Integration Calculator with Steps: Find Antiderivatives Instantly (2025)

📊 Stuck on $\int x^2\sin(x),dx$ and not sure which integration technique to use? You're not alone. Integration is one of the most challenging topics in calculus—but it doesn't have to be. Whether you're working through homework, preparing for exams, or just need to verify your work, an integration calculator with step-by-step solutions can be your secret weapon.

In this comprehensive guide, you'll learn everything about integration: what it is, key techniques, common mistakes, and how to use modern tools (including CAS-verified integration that prevents the errors pure AI tools make) to master this essential calculus skill.

🎯 What is Integration?

Integration is the reverse process of differentiation. While differentiation asks "what is the rate of change?", integration asks "what function has this rate of change?" or "what is the area under this curve?"

The Antiderivative Concept

An antiderivative of a function $f(x)$ is any function $F(x)$ whose derivative is $f(x)$. In symbols:

$$\text{If } F'(x) = f(x) \text{, then } F(x) \text{ is an antiderivative of } f(x)$$

For example, if $f(x) = 2x$, then $F(x) = x^2$ is an antiderivative because $\frac{d}{dx}(x^2) = 2x$.

But here's the catch: antiderivatives aren't unique. Since the derivative of a constant is zero, $F(x) = x^2 + 5$, $F(x) = x^2 - 3$, and $F(x) = x^2 + 100$ are all antiderivatives of $2x$. That's why we write the indefinite integral with a constant of integration:

$$\int 2x,dx = x^2 + C$$

Definite vs Indefinite Integrals

Indefinite Integral:

• Represents the general antiderivative (family of functions)
• Includes the constant $+C$
• Example: $\int x^2,dx = \frac{x^3}{3} + C$

Definite Integral:

• Represents a specific number (the area under the curve between two points)
• Uses limits of integration (lower and upper bounds)
• Example: $\int_0^2 x^2,dx = \frac{8}{3}$ (no $+C$ needed)

Geometric Interpretation

The definite integral $\int_a^b f(x),dx$ gives the signed area between the curve $y = f(x)$ and the $x$-axis from $x = a$ to $x = b$:

• Area above the $x$-axis contributes positive values
• Area below the $x$-axis contributes negative values

Real-World Applications

Integration isn't just abstract math—it's everywhere:

• Physics: Calculating work, energy, charge, fluid flow
• Engineering: Finding center of mass, moments of inertia
• Economics: Consumer surplus, total revenue from marginal revenue
• Probability: Finding probabilities from probability density functions
• Biology: Population growth models, drug concentration over time

📐 Integration Rules & Techniques

Mastering integration means knowing when and how to apply different techniques. Here are the fundamental rules and methods:

Power Rule for Integration

The most basic integration rule:

$$\int x^n,dx = \frac{x^{n+1}}{n+1} + C \quad (n \neq -1)$$

Examples:

• $\int x^2,dx = \frac{x^3}{3} + C$
• $\int x^5,dx = \frac{x^6}{6} + C$
• $\int \frac{1}{x^2},dx = \int x^{-2},dx = \frac{x^{-1}}{-1} + C = -\frac{1}{x} + C$

Special case: When $n = -1$, we get the natural logarithm:

$$\int \frac{1}{x},dx = \ln|x| + C$$

Constant Multiple Rule

Constants can be pulled out of the integral:

$$\int k \cdot f(x),dx = k \int f(x),dx$$

Example: $\int 5x^2,dx = 5\int x^2,dx = 5 \cdot \frac{x^3}{3} + C = \frac{5x^3}{3} + C$

Sum and Difference Rule

Integrate term by term:

$$\int [f(x) \pm g(x)],dx = \int f(x),dx \pm \int g(x),dx$$

Example:

$$\int (3x^2 + 2x - 5),dx = 3\int x^2,dx + 2\int x,dx - 5\int 1,dx = x^3 + x^2 - 5x + C$$

U-Substitution

The chain rule in reverse. Use when you have a composite function where the derivative of the "inside" function appears in the integrand.

Strategy:

1. Identify $u$ (usually the "inside" function)
2. Compute $du = u'(x),dx$
3. Rewrite the integral in terms of $u$
4. Integrate with respect to $u$
5. Substitute back to $x$

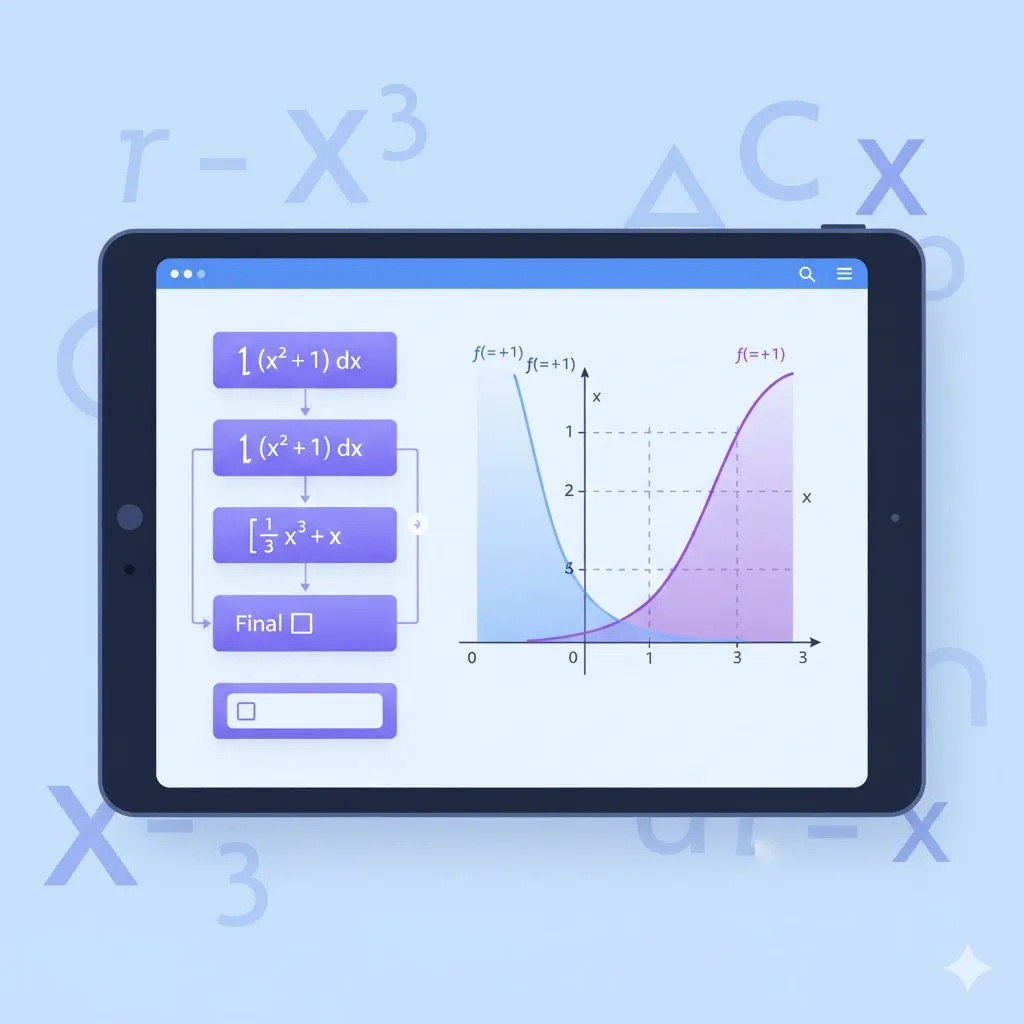
Example: $\int 2x(x^2 + 1)^5,dx$

Let $u = x^2 + 1$, then $du = 2x,dx$

$$\int 2x(x^2 + 1)^5,dx = \int u^5,du = \frac{u^6}{6} + C = \frac{(x^2+1)^6}{6} + C$$

Integration by Parts

Based on the product rule for derivatives. Use for products of functions where substitution doesn't work.

Formula:

$$\int u,dv = uv - \int v,du$$

Strategy (LIATE): Choose $u$ in order of priority:

• Logarithmic functions
• Inverse trig functions
• Algebraic functions (polynomials)
• Trigonometric functions
• Exponential functions

Example: $\int x e^x,dx$

Let $u = x$ (algebraic), $dv = e^x,dx$ Then $du = dx$, $v = e^x$

$$\int x e^x,dx = xe^x - \int e^x,dx = xe^x - e^x + C = e^x(x-1) + C$$

Trigonometric Integrals

Common Antiderivatives:

Function	Antiderivative
$\sin(x)$	$-\cos(x) + C$
$\cos(x)$	$\sin(x) + C$
$\sec^2(x)$	$\tan(x) + C$
$\sec(x)\tan(x)$	$\sec(x) + C$
$\csc^2(x)$	$-\cot(x) + C$
$\csc(x)\cot(x)$	$-\csc(x) + C$

Trig Identities for Integration:

For $\int \sin^2(x),dx$ or $\int \cos^2(x),dx$, use:

• $\sin^2(x) = \frac{1 - \cos(2x)}{2}$
• $\cos^2(x) = \frac{1 + \cos(2x)}{2}$

Common Antiderivatives Table

Function $f(x)$	Antiderivative $F(x)$
$k$ (constant)	$kx + C$
$x^n$	$\frac{x^{n+1}}{n+1} + C$ (if $n \neq -1$)
$\frac{1}{x}$	$\ln|x| + C$
$e^x$	$e^x + C$
$a^x$	$\frac{a^x}{\ln(a)} + C$
$\sin(x)$	$-\cos(x) + C$
$\cos(x)$	$\sin(x) + C$
$\sec^2(x)$	$\tan(x) + C$
$\frac{1}{\sqrt{1-x^2}}$	$\arcsin(x) + C$
$\frac{1}{1+x^2}$	$\arctan(x) + C$

Step-by-Step Integration Examples

Let's work through five examples covering different techniques:

Example 1: Basic Power Rule

Problem: Find $\int (3x^2 + 2x - 5),dx$

Solution:

Apply the power rule to each term:

$$\int (3x^2 + 2x - 5),dx = 3\int x^2,dx + 2\int x,dx - 5\int 1,dx$$

$$= 3 \cdot \frac{x^3}{3} + 2 \cdot \frac{x^2}{2} - 5x + C$$

$$= x^3 + x^2 - 5x + C$$

Check: Differentiate to verify: $\frac{d}{dx}(x^3 + x^2 - 5x + C) = 3x^2 + 2x - 5$ ✓

Example 2: U-Substitution

Problem: Find $\int 2x(x^2 + 1)^5,dx$

Solution:

Step 1: Identify the substitution. Notice that $2x$ is the derivative of $x^2 + 1$:

Let $u = x^2 + 1$

Step 2: Find $du$:

$$du = 2x,dx$$

Step 3: Rewrite the integral:

$$\int 2x(x^2 + 1)^5,dx = \int u^5,du$$

Step 4: Integrate:

$$\int u^5,du = \frac{u^6}{6} + C$$

Step 5: Substitute back:

$$= \frac{(x^2 + 1)^6}{6} + C$$

Check: Using the chain rule: $\frac{d}{dx}\left[\frac{(x^2+1)^6}{6}\right] = \frac{6(x^2+1)^5 \cdot 2x}{6} = 2x(x^2+1)^5$ ✓

Example 3: Integration by Parts

Problem: Find $\int x e^x,dx$

Solution:

Step 1: Choose $u$ and $dv$ using LIATE (algebraic before exponential):

$$u = x, \quad dv = e^x,dx$$

Step 2: Find $du$ and $v$:

$$du = dx, \quad v = e^x$$

Step 3: Apply integration by parts formula:

$$\int x e^x,dx = uv - \int v,du$$

$$= x \cdot e^x - \int e^x,dx$$

$$= xe^x - e^x + C$$

$$= e^x(x - 1) + C$$

Check: Using the product rule: $\frac{d}{dx}[e^x(x-1)] = e^x(x-1) + e^x \cdot 1 = xe^x$ ✓

Example 4: Definite Integral

Problem: Evaluate $\int_0^2 x^2,dx$

Solution:

Step 1: Find the antiderivative:

$$\int x^2,dx = \frac{x^3}{3}$$

Step 2: Apply the Fundamental Theorem of Calculus:

$$\int_0^2 x^2,dx = \left[\frac{x^3}{3}\right]_0^2 = \frac{2^3}{3} - \frac{0^3}{3} = \frac{8}{3} - 0 = \frac{8}{3}$$

Interpretation: The area under $y = x^2$ from $x = 0$ to $x = 2$ is $\frac{8}{3} \approx 2.667$ square units.

Example 5: Trig Integral with Identity

Problem: Find $\int \sin^2(x),dx$

Solution:

Step 1: Use the power-reduction identity:

$$\sin^2(x) = \frac{1 - \cos(2x)}{2}$$

Step 2: Substitute:

$$\int \sin^2(x),dx = \int \frac{1 - \cos(2x)}{2},dx$$

$$= \frac{1}{2}\int (1 - \cos(2x)),dx$$

$$= \frac{1}{2}\left[x - \frac{\sin(2x)}{2}\right] + C$$

$$= \frac{x}{2} - \frac{\sin(2x)}{4} + C$$

Check: Differentiate: $\frac{d}{dx}\left[\frac{x}{2} - \frac{\sin(2x)}{4}\right] = \frac{1}{2} - \frac{2\cos(2x)}{4} = \frac{1 - \cos(2x)}{2} = \sin^2(x)$ ✓

⚠️ Common Integration Mistakes

Even experienced students make these errors. Watch out for:

Mistake 1: Forgetting the Constant +C

Wrong: $\int x,dx = \frac{x^2}{2}$ Right: $\int x,dx = \frac{x^2}{2} + C$

Why it matters: Without $+C$, you're only finding one antiderivative, not the general family of antiderivatives.

Mistake 2: Wrong U-Substitution Choice

Problem: $\int x^2 e^{x^3},dx$

Wrong approach: Let $u = e^{x^3}$ (doesn't simplify the integral)

Right approach: Let $u = x^3$, so $du = 3x^2,dx$, which means $x^2,dx = \frac{1}{3}du$

$$\int x^2 e^{x^3},dx = \frac{1}{3}\int e^u,du = \frac{1}{3}e^u + C = \frac{1}{3}e^{x^3} + C$$

Mistake 3: Integration by Parts Product Choice

Problem: $\int x\ln(x),dx$

Wrong: Let $u = x$, $dv = \ln(x),dx$ (integrating $\ln(x)$ is harder than differentiating it)

Right: Let $u = \ln(x)$, $dv = x,dx$ (use LIATE: logarithmic before algebraic)

Mistake 4: Sign Errors in Trig Integrals

Wrong: $\int \sin(x),dx = \cos(x) + C$ Right: $\int \sin(x),dx = -\cos(x) + C$

Always remember: The derivative of $\cos(x)$ is $-\sin(x)$, so the antiderivative of $\sin(x)$ must include that negative sign.

Using MathPad for Integration

Modern integration calculators go beyond simple computation—they help you learn. Here's what sets MathPad apart:

CAS-Verified Symbolic Integration

The Problem with Pure AI: Large language models can make integration errors because they're pattern-matching, not computing symbolically. They might:

• Forget the constant $+C$
• Make sign errors in trig integrals
• Apply integration by parts incorrectly
• Get the wrong antiderivative for complex expressions

MathPad's Solution: Every integration step is verified by a Computer Algebra System (CAS):

1. AI proposes an integration technique
2. CAS verifies each step symbolically (not by pattern-matching)
3. If any step is wrong, CAS catches it before showing you
4. You only see mathematically verified, accurate solutions

This is why MathPad won't give you confident-sounding wrong answers like pure AI tools can. Every integration is symbolically verified. Learn more about our accuracy approach →

Step-by-Step Solutions

Don't just see the answer—understand the process:

• Which integration technique was used (power rule, u-substitution, by parts)
• Why that technique was chosen
• Every algebraic step from problem to solution
• Verification by differentiating the result

Math-Specific OCR

Typing complex integrals is tedious. MathPad uses cutting-edge OCR technology designed specifically for mathematical notation:

• Recognizes integral signs, bounds, variables
• Handles complex expressions like $\int \frac{x^2}{\sqrt{1-x^4}},dx$
• Reads handwritten math (not just printed textbook problems)
• Works from photos taken in any lighting condition

Additional Features for Learning Integration

Step Checker:

• Worked through a problem by hand?
• Photo your work and see if each integration step is correct
• Perfect for homework verification before submission

AI Tutor:

• "Why did you choose u-substitution here?"
• "How do I know when to use integration by parts?"
• "What's the geometric meaning of this integral?"
• Get instant answers to follow-up questions

Practice Problem Generator:

• Generate unlimited integration problems
• Focus on specific techniques (just u-substitution, just by parts)
• Adjustable difficulty levels
• Each problem comes with complete step-by-step solutions

Integration vs Differentiation

These are inverse operations, but they're not equally difficult:

Why Integration is Harder

Differentiation has clear rules:

• Power rule always works for polynomials
• Product rule, quotient rule, chain rule handle combinations
• Every differentiable function has exactly one derivative

Integration requires strategy:

• No single technique works for everything
• You must recognize which technique to use
• Some functions don't have closed-form antiderivatives
• Requires more creativity and pattern recognition

Verification by Differentiation

The best way to check your integration work: differentiate your answer. If you get back the original integrand, you're correct:

$$\text{If } F(x) = \int f(x),dx, \text{ then } F'(x) = f(x)$$

Example:

• You claim $\int 2x,dx = x^2 + C$
• Check: $\frac{d}{dx}(x^2 + C) = 2x$ ✓
• Correct!

Practice Problems

Test your integration skills with these problems:

Basic Problems

1. $\int (4x^3 - 3x^2 + 2),dx$
2. $\int (5x^4 + \frac{1}{x}),dx$

U-Substitution

3. $\int 6x^2(x^3 + 1)^4,dx$
4. $\int \frac{2x}{x^2 + 1},dx$

Integration by Parts

5. $\int x\sin(x),dx$
6. $\int x^2 e^x,dx$ (requires two applications)

Definite Integrals

7. $\int_1^3 (x^2 - 2x),dx$
8. $\int_0^\pi \sin(x),dx$

Ready to check your answers? Use MathPad's integration calculator to see step-by-step solutions for each problem. Try it now →

Frequently Asked Questions

What's the difference between definite and indefinite integrals?

An indefinite integral finds the general antiderivative (a family of functions that differ by a constant): $\int f(x),dx = F(x) + C$. A definite integral evaluates the antiderivative at specific bounds to get a number representing the signed area: $\int_a^b f(x),dx = F(b) - F(a)$.

How do I know which integration technique to use?

Start with this decision tree:

1. Simple polynomial or basic function? → Power rule
2. Derivative of inner function present? → U-substitution
3. Product of unrelated functions? → Integration by parts (use LIATE)
4. Trig powers? → Use trig identities first
5. Rational function? → Partial fractions (advanced)

With practice, pattern recognition becomes automatic.

Why is there a +C in indefinite integrals?

Since the derivative of any constant is zero, infinitely many functions have the same derivative. For example, $f(x) = x^2$, $f(x) = x^2 + 5$, and $f(x) = x^2 - 100$ all have derivative $2x$. The constant $C$ represents this infinite family of antiderivatives. For definite integrals, the constant cancels out: $(F(b) + C) - (F(a) + C) = F(b) - F(a)$.

Can all functions be integrated?

Every continuous function has an antiderivative, but not all antiderivatives can be expressed in terms of elementary functions (polynomials, trig, exponentials, logarithms). Famous examples:

• $\int e^{-x^2},dx$ (appears in probability, no closed form)
• $\int \frac{\sin(x)}{x},dx$ (sine integral function)
• $\int \frac{1}{\ln(x)},dx$ (logarithmic integral)

For these, we use numerical integration or special functions.

How do I check my integration answer?

Differentiate your result. If you get back the original integrand, you're correct:

Example: Is $\int 3x^2,dx = x^3 + C$ correct?

Check: $\frac{d}{dx}(x^3 + C) = 3x^2$ ✓ Yes!

This works because differentiation and integration are inverse operations.

What's u-substitution and when do I use it?

U-substitution is the chain rule in reverse. Use it when you have a composite function where the derivative of the inner function also appears in the integrand.

Example: $\int 2x(x^2 + 1)^5,dx$

• Inner function: $u = x^2 + 1$
• Its derivative: $du = 2x,dx$ (which appears in the integrand!)
• Substitute: $\int u^5,du = \frac{u^6}{6} + C = \frac{(x^2+1)^6}{6} + C$

Is integration harder than differentiation?

Yes, generally. Differentiation has straightforward rules that always work. Integration requires you to:

• Recognize which technique applies
• Sometimes try multiple approaches
• Use algebraic tricks and identities
• Accept that some integrals have no closed form

That's why practicing different problem types is essential for building intuition.

Do I need to memorize integration formulas?

You should memorize the basics:

• Power rule: $\int x^n,dx = \frac{x^{n+1}}{n+1} + C$
• Common trig antiderivatives ($\sin$, $\cos$, $\sec^2$)
• $\int e^x,dx = e^x + C$
• $\int \frac{1}{x},dx = \ln|x| + C$

For advanced techniques (by parts formula, trig identities), you can reference them—but understanding when to use them is more important than memorization.

Can AI solve integration problems?

AI can solve many integration problems, but pure AI tools can make mistakes because they use pattern-matching rather than symbolic computation. They might apply the wrong technique, forget constants, or make sign errors.

MathPad combines AI with CAS verification: AI proposes the solution method, then CAS verifies every step symbolically before showing you. This hybrid approach gives you AI's problem-solving abilities with mathematical certainty.

How does CAS verify integration symbolically?

CAS (Computer Algebra System) engines like SymPy perform exact symbolic manipulation, not numerical approximation:

1. Parses your integral into a mathematical expression tree
2. Applies integration rules algebraically (not by guessing patterns)
3. Verifies each transformation is mathematically valid
4. Checks the final answer by symbolic differentiation

This catches errors that pure AI might miss, ensuring every solution is mathematically correct. See our accuracy page for details →

🔗 Related Topics

Want to learn more calculus concepts?

• Derivative Calculator - Master differentiation (the inverse of integration)
• Understanding CAS Verification - How symbolic verification prevents math errors
• Khan Academy Calculus - Free video lessons on integration techniques

🎓 Conclusion

Integration is challenging, but with the right approach and tools, it becomes manageable. Remember:

✓ Master the fundamentals: Power rule, u-substitution, integration by parts ✓ Practice pattern recognition: Learn when to use each technique ✓ Always verify: Check your work by differentiating ✓ Use CAS-verified tools: Avoid the errors pure AI can make

Whether you're solving homework problems, preparing for exams, or just exploring calculus, MathPad's integration calculator gives you accurate, step-by-step solutions backed by symbolic verification.

Ready to solve your first integral? Start with MathPad's CAS-verified integration calculator →

---

Last updated: January 2025. All integration examples verified using Computer Algebra System (CAS) tools to ensure mathematical accuracy.