Need to find $\frac{d}{dx}$ of $x^3\sin(x)$ and not sure which rule to use? Calculus can feel overwhelming when you're first learning derivatives, but it doesn't have to be. Once you understand the basic rules, derivatives become a systematic process you can apply to any function.

This guide breaks down everything you need to know about derivatives—from the fundamental rules to complex applications—with real examples you can follow step-by-step.

💡 Pro tip: When faced with a complicated derivative, always identify which rule applies first (power, product, quotient, or chain rule). Breaking the problem into steps makes even the trickiest derivatives manageable.

What is a Derivative?

A derivative measures how a function changes as its input changes. In practical terms:

• Graphically: The derivative at a point is the slope of the tangent line to the function's curve at that point
• Physically: It represents rates of change—velocity (rate of change of position), acceleration (rate of change of velocity), etc.
• Mathematically: It's the limit of the slope of secant lines as two points get infinitesimally close

The derivative of a function $f(x)$ is written as:

• $f'(x)$ (Lagrange notation)
• $\frac{df}{dx}$ or $\frac{d}{dx}f(x)$ (Leibniz notation)
• $Df(x)$ (Euler notation)

Real-World Applications

Derivatives aren't just abstract math—they're everywhere:

• Physics: Velocity is the derivative of position; acceleration is the derivative of velocity
• Economics: Marginal cost is the derivative of total cost; marginal revenue is the derivative of revenue
• Biology: Population growth rates, spread of diseases
• Engineering: Optimization problems (maximizing strength, minimizing materials)
• Machine Learning: Gradient descent (training AI models) relies entirely on derivatives

Understanding derivatives is essential for any STEM field.

The Fundamental Differentiation Rules

Before we tackle complex derivatives, let's review the basic rules. These are the building blocks you'll use for everything else.

Power Rule

The most commonly used rule. For any constant $n$:

$$\frac{d}{dx}(x^n) = nx^{n-1}$$

Examples:

• $\frac{d}{dx}(x^3) = 3x^2$
• $\frac{d}{dx}(x^{10}) = 10x^9$
• $\frac{d}{dx}(\frac{1}{x}) = \frac{d}{dx}(x^{-1}) = -x^{-2} = -\frac{1}{x^2}$
• $\frac{d}{dx}(\sqrt{x}) = \frac{d}{dx}(x^{1/2}) = \frac{1}{2}x^{-1/2} = \frac{1}{2\sqrt{x}}$

Constant Multiple Rule

Constants come along for the ride:

$$\frac{d}{dx}(cf(x)) = c \cdot f'(x)$$

Example: $\frac{d}{dx}(5x^3) = 5 \cdot 3x^2 = 15x^2$

Sum/Difference Rule

Take derivatives term by term:

$$\frac{d}{dx}(f(x) \pm g(x)) = f'(x) \pm g'(x)$$

Example: $\frac{d}{dx}(x^3 + 2x^2 - 5x + 7) = 3x^2 + 4x - 5$

Product Rule

When multiplying two functions:

$$\frac{d}{dx}(f(x) \cdot g(x)) = f'(x) \cdot g(x) + f(x) \cdot g'(x)$$

Think: "derivative of first times second plus first times derivative of second"

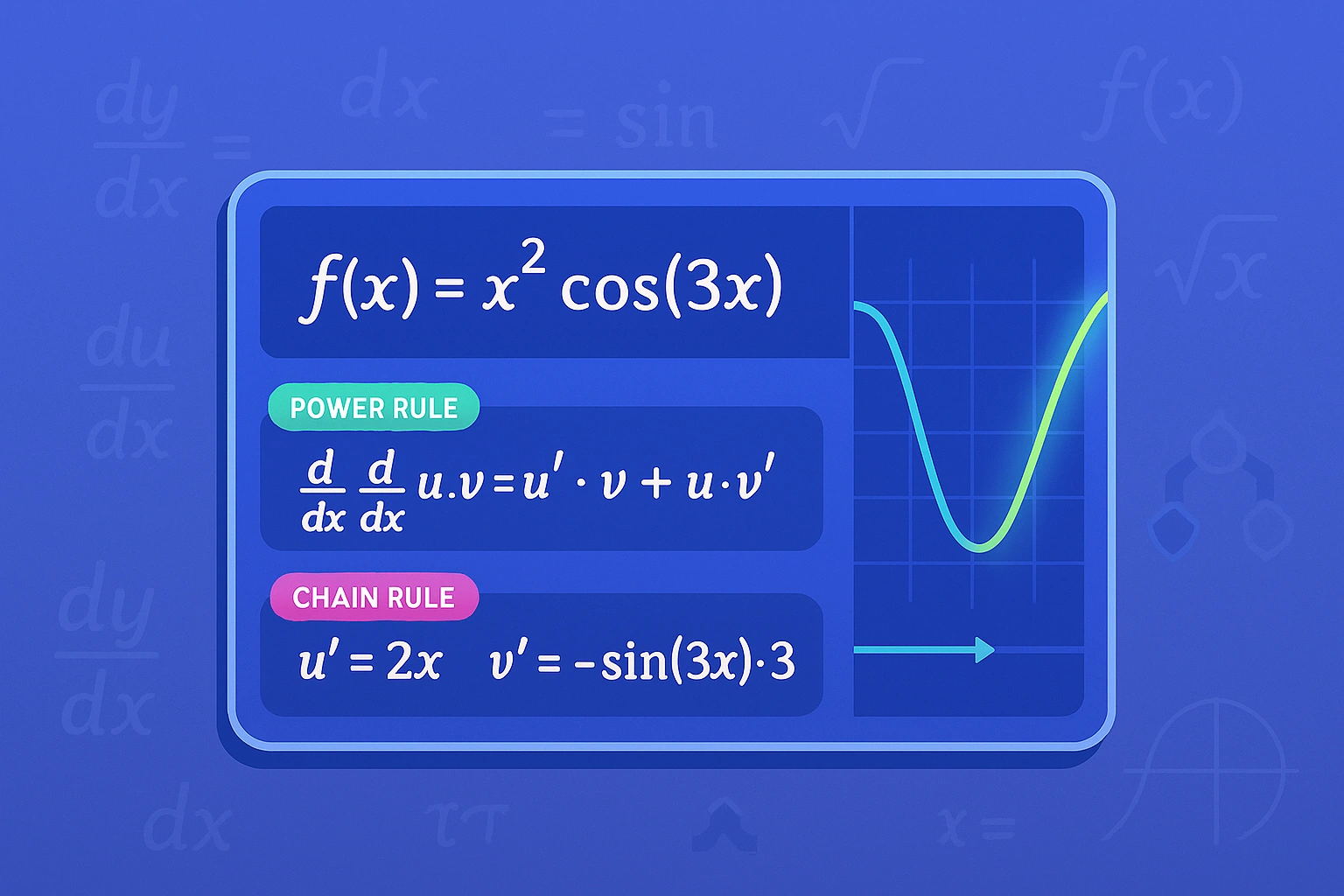
Example: $\frac{d}{dx}(x^2 \sin(x)) = 2x \sin(x) + x^2 \cos(x)$

Quotient Rule

When dividing two functions:

$$\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{f'(x) \cdot g(x) - f(x) \cdot g'(x)}{[g(x)]^2}$$

Think: "lo d-hi minus hi d-lo over lo-lo" (low derivative high minus high derivative low, over low squared)

Example: $\frac{d}{dx}\left(\frac{x^2}{x+1}\right) = \frac{2x(x+1) - x^2(1)}{(x+1)^2} = \frac{x^2 + 2x}{(x+1)^2}$

Chain Rule

For composite functions (function inside a function):

$$\frac{d}{dx}(f(g(x))) = f'(g(x)) \cdot g'(x)$$

Think: "derivative of outer function (with inside left alone) times derivative of inner function"

Example: $\frac{d}{dx}(\sin(x^2)) = \cos(x^2) \cdot 2x$

Common Function Derivatives

Memorize these—you'll use them constantly:

Exponential and Logarithmic:

• $\frac{d}{dx}(e^x) = e^x$
• $\frac{d}{dx}(\ln(x)) = \frac{1}{x}$
• $\frac{d}{dx}(a^x) = a^x \ln(a)$

Trigonometric:

• $\frac{d}{dx}(\sin(x)) = \cos(x)$
• $\frac{d}{dx}(\cos(x)) = -\sin(x)$
• $\frac{d}{dx}(\tan(x)) = \sec^2(x)$

Inverse Trigonometric:

• $\frac{d}{dx}(\arcsin(x)) = \frac{1}{\sqrt{1-x^2}}$
• $\frac{d}{dx}(\arctan(x)) = \frac{1}{1+x^2}$

Step-by-Step Examples

Let's work through five problems that demonstrate different techniques. Pay attention to which rule to use and why.

Example 1: Basic Polynomial

Problem: Find $\frac{d}{dx}(3x^4 - 2x^3 + 5x - 7)$

Solution:

1. Identify the rule: This is a polynomial, so use the power rule term by term

2. Apply the power rule to each term:

   • $\frac{d}{dx}(3x^4) = 3 \cdot 4x^3 = 12x^3$
   • $\frac{d}{dx}(-2x^3) = -2 \cdot 3x^2 = -6x^2$
   • $\frac{d}{dx}(5x) = 5 \cdot 1 = 5$
   • $\frac{d}{dx}(-7) = 0$ (constant)

3. Combine: $$\frac{d}{dx}(3x^4 - 2x^3 + 5x - 7) = 12x^3 - 6x^2 + 5$$

Answer: $12x^3 - 6x^2 + 5$

Example 2: Product Rule Application

Problem: Find $\frac{d}{dx}(x^3 \sin(x))$

Solution:

1. Identify the rule: This is a product of two functions, so use the product rule

2. Set up: Let $f(x) = x^3$ and $g(x) = \sin(x)$

3. Find derivatives:

   • $f'(x) = 3x^2$
   • $g'(x) = \cos(x)$

4. Apply product rule: $f'(x) \cdot g(x) + f(x) \cdot g'(x)$ $$= 3x^2 \cdot \sin(x) + x^3 \cdot \cos(x)$$

Answer: $3x^2 \sin(x) + x^3 \cos(x)$

Verification at a point: Let's check at $x = 0$:

• Original function: $f(0) = 0^3 \sin(0) = 0$
• Derivative: $f'(0) = 3(0)^2 \sin(0) + 0^3 \cos(0) = 0$
• This makes sense—the tangent line at the origin is horizontal for this function

Example 3: Chain Rule Application

Problem: Find $\frac{d}{dx}((3x^2 + 1)^5)$

Solution:

1. Identify the rule: This is a composite function—one function inside another—so use the chain rule

2. Identify outer and inner functions:

   • Outer: $f(u) = u^5$
   • Inner: $u = g(x) = 3x^2 + 1$

3. Find derivatives:

   • Outer: $f'(u) = 5u^4$
   • Inner: $g'(x) = 6x$

4. Apply chain rule: $f'(g(x)) \cdot g'(x)$ $$= 5(3x^2 + 1)^4 \cdot 6x$$ $$= 30x(3x^2 + 1)^4$$

Answer: $30x(3x^2 + 1)^4$

💡 Pro tip: For chain rule problems, always identify the "inside" function first. Then differentiate outside-in: derivative of outer (keeping inside unchanged) times derivative of inner.

Example 4: Quotient Rule Application

Problem: Find $\frac{d}{dx}\left(\frac{\sin(x)}{x^2 + 1}\right)$

Solution:

1. Identify the rule: This is one function divided by another, so use the quotient rule

2. Set up: Let $f(x) = \sin(x)$ (numerator) and $g(x) = x^2 + 1$ (denominator)

3. Find derivatives:

   • $f'(x) = \cos(x)$
   • $g'(x) = 2x$

4. Apply quotient rule: $\frac{f'(x) \cdot g(x) - f(x) \cdot g'(x)}{[g(x)]^2}$ $$= \frac{\cos(x)(x^2 + 1) - \sin(x)(2x)}{(x^2 + 1)^2}$$

5. Simplify (optional): $$= \frac{x^2\cos(x) + \cos(x) - 2x\sin(x)}{(x^2 + 1)^2}$$

Answer: $\frac{x^2\cos(x) + \cos(x) - 2x\sin(x)}{(x^2 + 1)^2}$

Example 5: Mixed Rules (Complex)

Problem: Find $\frac{d}{dx}(e^{x^2} \cdot \cos(3x))$

Solution:

1. Identify the rules: This requires both product rule and chain rule

2. Set up for product rule:

   • $f(x) = e^{x^2}$
   • $g(x) = \cos(3x)$

3. Find $f'(x)$ using chain rule:

   • Outer: $e^u$ with derivative $e^u$
   • Inner: $u = x^2$ with derivative $2x$
   • $f'(x) = e^{x^2} \cdot 2x = 2xe^{x^2}$

4. Find $g'(x)$ using chain rule:

   • Outer: $\cos(u)$ with derivative $-\sin(u)$
   • Inner: $u = 3x$ with derivative $3$
   • $g'(x) = -\sin(3x) \cdot 3 = -3\sin(3x)$

5. Apply product rule: $f'(x) \cdot g(x) + f(x) \cdot g'(x)$ $$= 2xe^{x^2} \cdot \cos(3x) + e^{x^2} \cdot (-3\sin(3x))$$ $$= 2xe^{x^2}\cos(3x) - 3e^{x^2}\sin(3x)$$

6. Factor (optional): $$= e^{x^2}(2x\cos(3x) - 3\sin(3x))$$

Answer: $e^{x^2}(2x\cos(3x) - 3\sin(3x))$

Common Derivative Mistakes

Mistake 1: Forgetting the Chain Rule

Wrong: $\frac{d}{dx}(\sin(3x)) = \cos(3x)$ ❌

Right: $\frac{d}{dx}(\sin(3x)) = \cos(3x) \cdot 3 = 3\cos(3x)$ ✓

Always multiply by the derivative of the inside function!

Mistake 2: Sign Errors in Quotient Rule

Wrong: Using $\frac{f'g + fg'}{g^2}$ instead of $\frac{f'g - fg'}{g^2}$ ❌

Right: The quotient rule is minus in the middle: "lo d-hi minus hi d-lo over lo-lo" ✓

Mistake 3: Mixing Up Trig Derivatives

Wrong: $\frac{d}{dx}(\cos(x)) = \sin(x)$ ❌

Right: $\frac{d}{dx}(\cos(x)) = -\sin(x)$ ✓ (note the negative sign)

Common mix-ups:

• $\sin'(x) = \cos(x)$ ✓
• $\cos'(x) = -\sin(x)$ ✓ (negative!)
• $\tan'(x) = \sec^2(x)$ ✓ (not $\tan^2$!)

Mistake 4: Product Rule Error

Wrong: $\frac{d}{dx}(f \cdot g) = f' \cdot g'$ ❌ (treating it like a chain rule)

Right: $\frac{d}{dx}(f \cdot g) = f' \cdot g + f \cdot g'$ ✓

You can't just multiply the derivatives—you need both terms!

How to Check Your Derivative

Wondering if your derivative is correct? Here are three verification methods:

Method 1: Numerical Verification

Use the definition of derivative: $f'(x) \approx \frac{f(x+h) - f(x)}{h}$ for small $h$

Example: For $f(x) = x^2$ at $x = 3$:

• We know $f'(x) = 2x$, so $f'(3) = 6$
• Numerical: $\frac{f(3.001) - f(3)}{0.001} = \frac{9.006001 - 9}{0.001} = 6.001 \approx 6$ ✓

Method 2: Graphing Comparison

Plot both $f(x)$ and $f'(x)$. Check if:

• Where $f$ is increasing, $f' > 0$
• Where $f$ is decreasing, $f' < 0$
• Where $f$ has a horizontal tangent (peak/valley), $f' = 0$

Method 3: Use MathPad's Step Checker

Input your step-by-step solution and let MathPad verify each step. This catches algebraic errors and shows you exactly where any mistake occurred.

Using MathPad for Derivatives

Learning derivatives takes practice—lots of it. Here's how MathPad accelerates your mastery:

CAS-Verified Symbolic Differentiation

Here's the critical advantage: AI models can make mistakes with derivatives, especially on complex chain rule or product rule problems. MathPad combines AI with a Computer Algebra System (CAS) that performs true symbolic differentiation.

What this means for you:

• Every derivative is symbolically verified, not pattern-matched
• No sign errors in quotient rule applications
• No forgotten chain rule multiplications
• Complex derivatives like $\frac{d}{dx}(e^{x^2}\cos(3x))$ are handled perfectly

This is the same CAS engine that powers Mathematica and Wolfram Alpha—but integrated with AI tutoring. Learn more about our accuracy approach →

How MathPad Helps You Master Calculus

1. SnapSolve for textbook problems: Math-specific OCR (not generic text recognition) reads complex calculus notation instantly
2. Step-by-step solutions: See every application of every rule, CAS-verified at each step
3. Step Checker for homework: Compare your solution process against the correct method to understand mistakes
4. AI Tutor for questions: Ask "why do I use chain rule here?" or "how do I know when to use quotient rule vs product rule?"
5. Practice problem generator: Get unlimited derivative problems tailored to specific rules you're practicing

Try solving derivatives in MathPad →

Practice Problems

Ready to test your skills? Try these problems, organized by difficulty. Show all your work, identifying which rule you're using at each step.

Basic (Power Rule):

1. $\frac{d}{dx}(5x^4 - 3x^2 + 7)$
2. $\frac{d}{dx}(\sqrt{x} + \frac{1}{x^2})$

Intermediate (Product/Quotient Rule): 3. $\frac{d}{dx}(x^2 \cos(x))$ 4. $\frac{d}{dx}\left(\frac{x^3}{x^2 + 1}\right)$

Advanced (Chain Rule + Mixed): 5. $\frac{d}{dx}(\sin^2(x))$ (Hint: rewrite as $(\sin(x))^2$) 6. $\frac{d}{dx}(e^{\sin(x)})$

Want instant step-by-step solutions? Solve these in MathPad and see detailed explanations showing which rules apply at each step.

Frequently Asked Questions

What does a derivative actually tell you?

A derivative tells you the instantaneous rate of change of a function at a specific point. Geometrically, it's the slope of the tangent line. Physically, if $f(t)$ is position, then $f'(t)$ is velocity—how fast position is changing. The derivative answers "how is this quantity changing right now?"

Do I need to memorize all the derivative rules?

You should memorize the basic rules (power, product, quotient, chain) and common derivatives (trig, exponential, log). With practice, these become second nature. Advanced formulas can be looked up, but if you're constantly looking up the product rule, you'll struggle on exams and in applications.

When do I use the product rule vs the chain rule?

• Product rule: When you have two functions multiplied together, like $x^2 \sin(x)$
• Chain rule: When you have one function inside another (composition), like $\sin(x^2)$

If it's $(f \cdot g)$, use product rule. If it's $f(g(x))$, use chain rule. Sometimes you need both!

Why is the derivative of a constant zero?

A constant function like $f(x) = 5$ has a horizontal graph. The slope of a horizontal line is zero—it's not changing at all. Mathematically: $\frac{d}{dx}(c) = \lim_{h \to 0} \frac{c - c}{h} = \lim_{h \to 0} \frac{0}{h} = 0$

Can I always use the power rule?

The power rule works for any function of the form $x^n$ where $n$ is a constant (including fractions and negative numbers). But it doesn't work for functions like $e^x$, $\sin(x)$, or $\ln(x)$—those have their own derivative rules.

What's the difference between $\frac{dy}{dx}$ and $\frac{d}{dx}$?

$\frac{dy}{dx}$ is the derivative of $y$ with respect to $x$ (a specific result). $\frac{d}{dx}$ is the differentiation operator (an instruction to take a derivative). Think of $\frac{d}{dx}$ as the "action" and $\frac{dy}{dx}$ as the "result."

How do I know which rule to use first on complicated problems?

Work from the outside in. Look at the outermost operation:

• If the whole thing is a product, start with product rule
• If it's a quotient, start with quotient rule
• If it's a composition (one function of another), start with chain rule
• Once you identify the outer operation, apply that rule, which will require taking derivatives of simpler pieces

Why do we learn derivatives if calculators can do them?

The same reason you learn arithmetic even though calculators exist—understanding the process is crucial for problem-solving. Derivatives are tools for optimization, analyzing motion, understanding rates of change, and building mathematical models. You need to understand when to take a derivative and what it means, not just how to mechanically compute it.

What if my answer looks different from the solution manual?

Derivatives can be written in many equivalent forms. For example:

• $\frac{2x}{(x^2+1)^2}$ is the same as $2x(x^2+1)^{-2}$
• $\frac{1}{2\sqrt{x}}$ is the same as $\frac{1}{2}x^{-1/2}$ or $\frac{\sqrt{x}}{2x}$

To check equivalence, simplify both forms or plug in a specific value for $x$.

How do I get faster at taking derivatives?

Practice is key, but smart practice is better:

1. Do 5-10 problems of one type (e.g., product rule) until it's automatic
2. Mix problem types to practice identifying which rule to use
3. Time yourself to build speed
4. Use tools like MathPad to check your work immediately so you learn from mistakes right away

Related Topics

Want to deepen your calculus knowledge? Check out these related guides:

• Integration Techniques: The Reverse of Derivatives (coming soon)
• Implicit Differentiation: When y Can't Be Isolated (coming soon)
• Applications of Derivatives: Optimization and Related Rates (coming soon)
• Khan Academy: Calculus 1 - Free video lessons
• Paul's Online Math Notes - Comprehensive calculus guide
• See all MathPad features - AI Tutor, Step Checker, and practice generators

Conclusion

Derivatives are the foundation of calculus, and mastering them opens doors to advanced mathematics, physics, engineering, and beyond. The key is understanding which rule applies when, and that comes from practice and pattern recognition.

Don't get discouraged if it feels mechanical at first—with enough practice, you'll start recognizing patterns instantly. Soon you'll be taking derivatives as automatically as you do basic arithmetic.

If you want to accelerate your learning with instant feedback and step-by-step explanations for every derivative, try MathPad's free version and experience AI-powered calculus tutoring.

---

Have questions about derivatives? Contact our team or start solving problems at mathpad.ai/app.