Struggling with $\lim_{x \to 0} \frac{\sin(x)}{x}$ and getting an indeterminate form $\frac{0}{0}$? You're not alone. Limits are the foundation of calculus—they define derivatives, integrals, and continuity. Understanding limits isn't just about passing your calculus exam; it's about grasping the fundamental concept that makes all of calculus work.

This comprehensive guide will teach you everything about limits: what they are, how to evaluate them, when to use L'Hôpital's rule, and how to avoid common mistakes—with real examples you can follow step-by-step.

🎯 Try it now: Use our free interactive Limit Calculator to evaluate limits instantly with step-by-step solutions for indeterminate forms and L'Hôpital's rule.

💡 Pro tip: When evaluating a limit, always try direct substitution first. If that gives you a determinate value (not $\frac{0}{0}$ or $\frac{\infty}{\infty}$), you're done! Only use advanced techniques for indeterminate forms.

---

📸 Ready to get unstuck? Try MathPad Free →

---

What is a Limit?

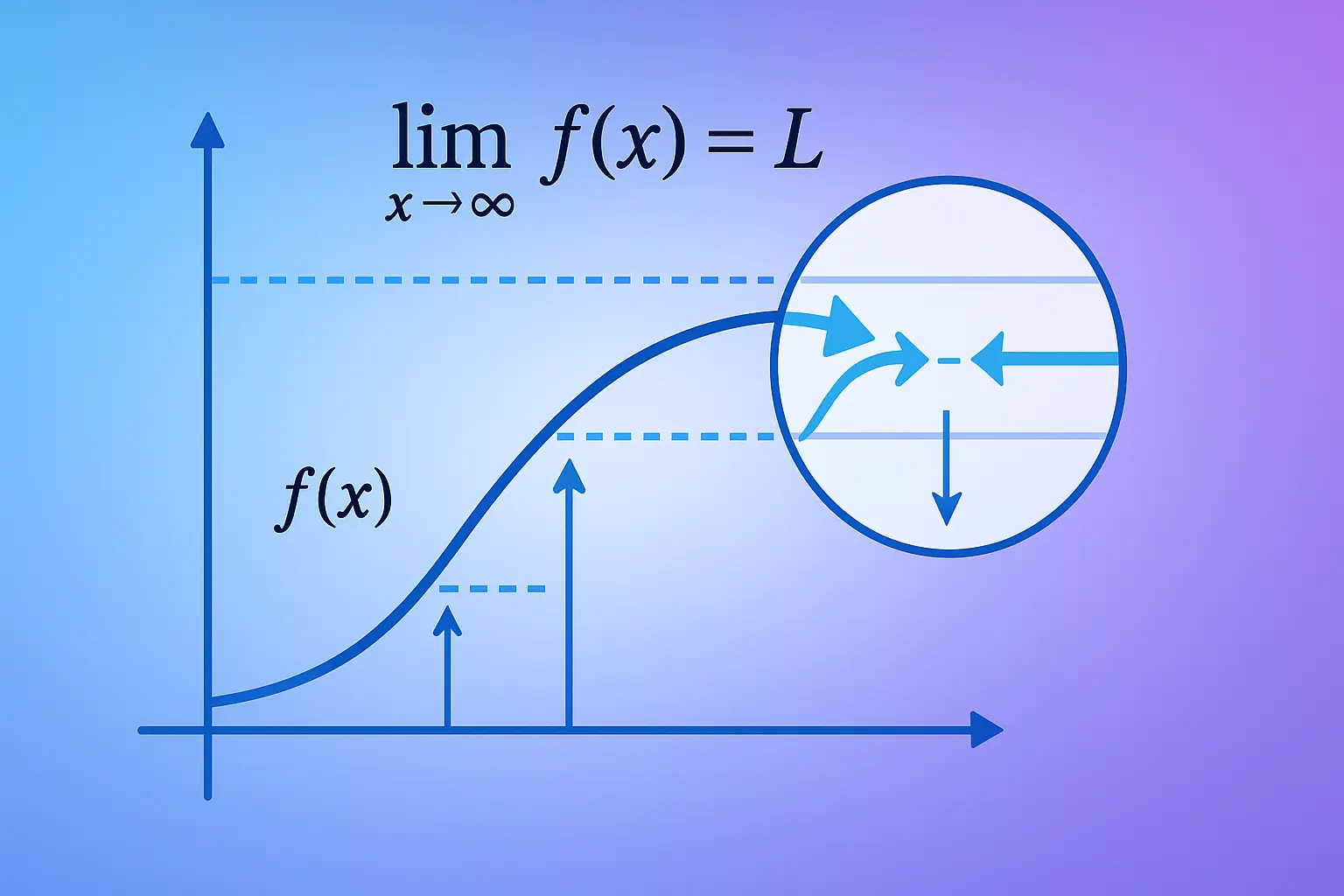
A limit describes what value a function approaches as the input approaches a specific point. The formal notation:

$$\lim_{x \to a} f(x) = L$$

This reads: "The limit of $f(x)$ as $x$ approaches $a$ is $L$"

Key insight: The limit describes the function's behavior near a point, not necessarily at the point. The function doesn't even need to be defined at $x = a$ for the limit to exist!

Intuitive Understanding

Think of driving toward a city on the highway:

• $x$: Your current position
• $a$: The city's location
• $f(x)$: The elevation at your position
• $\lim_{x \to a} f(x)$: What elevation you're approaching (even if there's a bridge out before you reach it)

You can get arbitrarily close to the city and observe what elevation you're heading toward, regardless of whether you can actually reach it.

Formal Definition (ε-δ Definition)

For the mathematically curious, here's the rigorous definition:

$$\lim_{x \to a} f(x) = L \text{ means: } \forall \varepsilon > 0, \exists \delta > 0 \text{ such that if } 0 < |x - a| < \delta, \text{ then } |f(x) - L| < \varepsilon$$

Translation: No matter how close to $L$ you want to get ($\varepsilon$), we can find a zone around $a$ ($\delta$) where $f(x)$ stays within your desired tolerance.

Why Limits Matter

Limits are the foundation of:

• Derivatives: $f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}$
• Integrals: Defined as limits of Riemann sums
• Continuity: $f$ is continuous at $a$ if $\lim_{x \to a} f(x) = f(a)$
• Series convergence: $\sum_{n=1}^{\infty} a_n = \lim_{N \to \infty} \sum_{n=1}^{N} a_n$

Real-world applications:

• Physics: Instantaneous velocity (limit of average velocity)
• Engineering: Asymptotic behavior of systems
• Economics: Marginal analysis (infinitesimal changes)
• Computer Science: Algorithm complexity (behavior as $n \to \infty$)

Types of Limits

One-Sided Limits

Sometimes a function approaches different values from the left and right:

Right-hand limit (from the right): $$\lim_{x \to a^+} f(x) = L \quad \text{(approach from } x > a \text{)}$$

Left-hand limit (from the left): $$\lim_{x \to a^-} f(x) = M \quad \text{(approach from } x < a \text{)}$$

Example: For $f(x) = \frac{|x|}{x}$:

• $\lim_{x \to 0^+} f(x) = 1$ (from the right, $|x| = x$, so $\frac{x}{x} = 1$)
• $\lim_{x \to 0^-} f(x) = -1$ (from the left, $|x| = -x$, so $\frac{-x}{x} = -1$)

The two-sided limit $\lim_{x \to 0} f(x)$ does not exist because the one-sided limits don't agree.

Limits at Infinity

Describes behavior as $x$ gets arbitrarily large:

$$\lim_{x \to \infty} f(x) = L \quad \text{or} \quad \lim_{x \to -\infty} f(x) = L$$

Example: $\lim_{x \to \infty} \frac{1}{x} = 0$ (as $x$ grows, $\frac{1}{x}$ shrinks toward zero)

Infinite Limits

Describes unbounded behavior:

$$\lim_{x \to a} f(x) = \infty \quad \text{(or } -\infty \text{)}$$

Example: $\lim_{x \to 0^+} \frac{1}{x^2} = \infty$ (as $x$ approaches 0 from the right, $\frac{1}{x^2}$ grows without bound)

Note: This technically means the limit "does not exist" in the finite sense, but we specify how it fails (by growing infinitely).

Evaluating Limits: Core Techniques

Technique 1: Direct Substitution

Always start here! If $f$ is continuous at $a$, then:

$$\lim_{x \to a} f(x) = f(a)$$

Example: Find $\lim_{x \to 2} (x^2 + 3x - 1)$

Solution: Substitute directly: $2^2 + 3(2) - 1 = 4 + 6 - 1 = 9$ ✓

Technique 2: Factoring

Use when direct substitution gives $\frac{0}{0}$ (indeterminate form):

Example: Find $\lim_{x \to 2} \frac{x^2 - 4}{x - 2}$

Solution:

1. Direct substitution: $\frac{2^2 - 4}{2 - 2} = \frac{0}{0}$ (indeterminate)
2. Factor numerator: $x^2 - 4 = (x-2)(x+2)$
3. Cancel common factor: $$\lim_{x \to 2} \frac{(x-2)(x+2)}{x-2} = \lim_{x \to 2} (x+2)$$
4. Now substitute: $2 + 2 = 4$

Answer: $\lim_{x \to 2} \frac{x^2 - 4}{x - 2} = 4$

Technique 3: Rationalizing

Use for limits with square roots:

Example: Find $\lim_{x \to 0} \frac{\sqrt{x+4} - 2}{x}$

Solution:

1. Direct substitution: $\frac{\sqrt{0+4} - 2}{0} = \frac{0}{0}$ (indeterminate)
2. Multiply by conjugate: $$\lim_{x \to 0} \frac{\sqrt{x+4} - 2}{x} \cdot \frac{\sqrt{x+4} + 2}{\sqrt{x+4} + 2}$$
3. Simplify numerator: $$= \lim_{x \to 0} \frac{(x+4) - 4}{x(\sqrt{x+4} + 2)} = \lim_{x \to 0} \frac{x}{x(\sqrt{x+4} + 2)}$$
4. Cancel $x$: $$= \lim_{x \to 0} \frac{1}{\sqrt{x+4} + 2} = \frac{1}{2 + 2} = \frac{1}{4}$$

Answer: $\frac{1}{4}$

Technique 4: L'Hôpital's Rule

When to use: For indeterminate forms $\frac{0}{0}$ or $\frac{\infty}{\infty}$

The rule: If $\lim_{x \to a} f(x) = \lim_{x \to a} g(x) = 0$ (or both $\infty$), then:

$$\lim_{x \to a} \frac{f(x)}{g(x)} = \lim_{x \to a} \frac{f'(x)}{g'(x)}$$

(provided the right side exists)

Example: Find $\lim_{x \to 0} \frac{\sin(x)}{x}$

Solution:

1. Check form: $\frac{\sin(0)}{0} = \frac{0}{0}$ ✓ (indeterminate)
2. Apply L'Hôpital's: Take derivatives of numerator and denominator $$\lim_{x \to 0} \frac{\sin(x)}{x} = \lim_{x \to 0} \frac{\cos(x)}{1} = \cos(0) = 1$$

Answer: 1 (This is a famous limit!)

Technique 5: Squeeze Theorem

When to use: When you can "trap" the function between two simpler functions

The theorem: If $g(x) \leq f(x) \leq h(x)$ near $a$, and $\lim_{x \to a} g(x) = \lim_{x \to a} h(x) = L$, then:

$$\lim_{x \to a} f(x) = L$$

Example: Find $\lim_{x \to 0} x^2 \sin\left(\frac{1}{x}\right)$

Solution:

We know $-1 \leq \sin\left(\frac{1}{x}\right) \leq 1$ always

Multiply by $x^2 \geq 0$:

$$-x^2 \leq x^2\sin\left(\frac{1}{x}\right) \leq x^2$$

Both $\lim_{x \to 0} (-x^2) = 0$ and $\lim_{x \to 0} x^2 = 0$

By squeeze theorem: $\lim_{x \to 0} x^2\sin\left(\frac{1}{x}\right) = 0$

Step-by-Step Examples

Example 1: Basic Polynomial Limit

Problem: Find $\lim_{x \to 3} (2x^2 - 5x + 1)$

Solution:

Since polynomials are continuous everywhere, use direct substitution:

$$\lim_{x \to 3} (2x^2 - 5x + 1) = 2(3)^2 - 5(3) + 1 = 18 - 15 + 1 = 4$$

Answer: 4

Example 2: Indeterminate Form (Factoring)

Problem: Find $\lim_{x \to -1} \frac{x^2 + 3x + 2}{x + 1}$

Solution:

Step 1: Try direct substitution: $$\frac{(-1)^2 + 3(-1) + 2}{-1 + 1} = \frac{1 - 3 + 2}{0} = \frac{0}{0}$$

Indeterminate form—we need to simplify.

Step 2: Factor the numerator: $$x^2 + 3x + 2 = (x+1)(x+2)$$

Step 3: Cancel common factors: $$\lim_{x \to -1} \frac{(x+1)(x+2)}{x+1} = \lim_{x \to -1} (x+2)$$

Step 4: Now substitute: $$-1 + 2 = 1$$

Answer: 1

Verification: The original function has a removable discontinuity (hole) at $x = -1$, but the limit exists.

Example 3: Limit at Infinity (Rational Function)

Problem: Find $\lim_{x \to \infty} \frac{3x^2 + 2x - 5}{x^2 + 1}$

Solution:

Strategy: Divide numerator and denominator by highest power of $x$ (which is $x^2$):

$$\lim_{x \to \infty} \frac{3x^2 + 2x - 5}{x^2 + 1} = \lim_{x \to \infty} \frac{\frac{3x^2}{x^2} + \frac{2x}{x^2} - \frac{5}{x^2}}{\frac{x^2}{x^2} + \frac{1}{x^2}}$$

$$= \lim_{x \to \infty} \frac{3 + \frac{2}{x} - \frac{5}{x^2}}{1 + \frac{1}{x^2}}$$

As $x \to \infty$: $\frac{2}{x} \to 0$, $\frac{5}{x^2} \to 0$, $\frac{1}{x^2} \to 0$

$$= \frac{3 + 0 - 0}{1 + 0} = 3$$

Answer: 3

Interpretation: The horizontal asymptote of the function is $y = 3$.

Example 4: L'Hôpital's Rule Application

Problem: Find $\lim_{x \to 0} \frac{e^x - 1}{x}$

Solution:

Step 1: Check the form: $$\frac{e^0 - 1}{0} = \frac{1 - 1}{0} = \frac{0}{0}$$ ✓ (indeterminate)

Step 2: Apply L'Hôpital's rule (differentiate top and bottom): $$\lim_{x \to 0} \frac{e^x - 1}{x} = \lim_{x \to 0} \frac{\frac{d}{dx}(e^x - 1)}{\frac{d}{dx}(x)} = \lim_{x \to 0} \frac{e^x}{1}$$

Step 3: Substitute: $$= e^0 = 1$$

Answer: 1

Note: This is actually the definition of the derivative of $e^x$ at $x = 0$!

Example 5: One-Sided Limit

Problem: Find $\lim_{x \to 0^+} \frac{1}{x}$ and $\lim_{x \to 0^-} \frac{1}{x}$

Solution:

Right-hand limit (approaching from positive values):

As $x \to 0^+$, $x$ is a small positive number, so $\frac{1}{x}$ is a large positive number.

$$\lim_{x \to 0^+} \frac{1}{x} = +\infty$$

Left-hand limit (approaching from negative values):

As $x \to 0^-$, $x$ is a small negative number, so $\frac{1}{x}$ is a large negative number.

$$\lim_{x \to 0^-} \frac{1}{x} = -\infty$$

Conclusion: Since the one-sided limits don't agree, the two-sided limit $\lim_{x \to 0} \frac{1}{x}$ does not exist.

---

📸 Ready to get unstuck? Try MathPad Free →

---

Common Indeterminate Forms

Some limit expressions initially appear "undefined" but can be evaluated with proper techniques:

Form	Example	Technique
$\frac{0}{0}$	$\lim_{x \to 2} \frac{x^2-4}{x-2}$	Factor, L'Hôpital's
$\frac{\infty}{\infty}$	$\lim_{x \to \infty} \frac{x^2}{e^x}$	L'Hôpital's, comparison
$0 \cdot \infty$	$\lim_{x \to \infty} x \cdot e^{-x}$	Rewrite as $\frac{x}{e^x}$
$\infty - \infty$	$\lim_{x \to \infty} (x - \sqrt{x^2+x})$	Rationalize, combine
$0^0$, $1^\infty$, $\infty^0$	$\lim_{x \to 0^+} x^x$	Take logarithm

Non-indeterminate forms (these have definite values):

• $\frac{c}{0^+} = +\infty$ (where $c > 0$)
• $\frac{c}{0^-} = -\infty$ (where $c > 0$)
• $\frac{c}{\infty} = 0$
• $\infty + \infty = \infty$

Common Mistakes to Avoid

Mistake 1: Using L'Hôpital's When It Doesn't Apply

Wrong: Applying L'Hôpital's to $\lim_{x \to 1} \frac{x^2 + 1}{x + 1}$ ❌

This gives $\frac{1 + 1}{1 + 1} = \frac{2}{2} = 1$, which is not indeterminate. Just substitute directly: $\frac{1^2 + 1}{1 + 1} = 1$ ✓

Rule: Only use L'Hôpital's for $\frac{0}{0}$ or $\frac{\infty}{\infty}$ forms!

Mistake 2: Confusing Limit with Function Value

Wrong: Thinking $\lim_{x \to 2} \frac{x^2-4}{x-2} = \frac{0}{0}$ (undefined) ❌

Right: The limit is 4, even though the function is undefined at $x = 2$ ✓

The limit describes behavior near the point, not at the point.

Mistake 3: Incorrect Infinity Arithmetic

Wrong: $\infty - \infty = 0$ ❌

Right: $\infty - \infty$ is indeterminate—it could be anything! ✓

Example:

• $\lim_{x \to \infty} (x - x) = 0$
• $\lim_{x \to \infty} (x^2 - x) = \infty$
• $\lim_{x \to \infty} (x - x^2) = -\infty$

All are "$\infty - \infty$" forms with different answers.

Mistake 4: Misapplying L'Hôpital's Rule

Wrong: For $\lim_{x \to 0} \frac{\sin(x)}{x}$, taking derivative of the entire fraction: $\frac{d}{dx}\left[\frac{\sin(x)}{x}\right]$ ❌

Right: Take derivatives of numerator and denominator separately: $\frac{\frac{d}{dx}[\sin(x)]}{\frac{d}{dx}[x]} = \frac{\cos(x)}{1}$ ✓

Using MathPad for Limits

Evaluating limits combines pattern recognition, algebraic manipulation, and calculus rules—plenty of room for mistakes. Here's how MathPad helps:

CAS-Verified Limit Evaluation

The problem with pure AI: Language models can make errors when evaluating limits because they're guessing patterns, not performing symbolic computation. They might:

• Misidentify indeterminate forms
• Apply L'Hôpital's rule incorrectly
• Make algebraic errors when factoring or simplifying
• Give wrong answers for one-sided limits

MathPad's solution: Every limit is verified by a Computer Algebra System (CAS):

1. AI proposes the evaluation strategy
2. CAS verifies each algebraic step symbolically
3. CAS computes the limit using rigorous algorithms (not pattern-matching)
4. You get mathematically verified solutions

This means no confident-but-wrong answers. Every limit is symbolically correct. Learn more about our accuracy approach →

How MathPad Accelerates Learning

1. SnapSolve for textbook problems: Math-specific OCR reads complex limit notation instantly
2. Step-by-step solutions: See exactly which technique to use and why
3. Step Checker for homework: Input your work and verify each step
4. AI Tutor for understanding: Ask "Why is this $\frac{0}{0}$?" or "When should I use L'Hôpital's?"
5. Practice problems: Generate unlimited limit problems organized by technique

Try solving limits in MathPad →

Practice Problems

Test your limit evaluation skills with these problems:

Direct Substitution:

1. $\lim_{x \to 2} (3x^2 - 4x + 1)$
2. $\lim_{x \to 0} \cos(x)$

Factoring: 3. $\lim_{x \to 3} \frac{x^2 - 9}{x - 3}$ 4. $\lim_{x \to -2} \frac{x^2 + 5x + 6}{x + 2}$

Limits at Infinity: 5. $\lim_{x \to \infty} \frac{2x^3 + x}{x^3 - 5}$ 6. $\lim_{x \to \infty} \frac{5x^2 + 3}{x^3 + 1}$

L'Hôpital's Rule: 7. $\lim_{x \to 0} \frac{\tan(x)}{x}$ 8. $\lim_{x \to \infty} \frac{\ln(x)}{x}$

One-Sided Limits: 9. $\lim_{x \to 0^+} \frac{\sqrt{x}}{x}$ 10. $\lim_{x \to 2^-} \frac{1}{x - 2}$

Want instant step-by-step solutions? Solve these in MathPad and see detailed explanations for each technique.

Frequently Asked Questions

What does "limit does not exist" mean?

A limit fails to exist when:

1. One-sided limits disagree: $\lim_{x \to a^+} f(x) \neq \lim_{x \to a^-} f(x)$
2. Function oscillates: Like $\sin\left(\frac{1}{x}\right)$ as $x \to 0$
3. Unbounded behavior: Like $\lim_{x \to 0} \frac{1}{x^2} = \infty$ (technically "does not exist" as a finite value)

When should I use L'Hôpital's rule?

Only for indeterminate forms: $\frac{0}{0}$ or $\frac{\infty}{\infty}$. Always check the form first by substituting. If it's not indeterminate, L'Hôpital's doesn't apply. Other forms like $0 \cdot \infty$ need to be rewritten as fractions first.

Can a limit exist even if the function is undefined at that point?

Yes! Limits describe behavior near a point, not at the point. Example: $\lim_{x \to 2} \frac{x^2-4}{x-2} = 4$ even though the function is undefined at $x = 2$. This is a removable discontinuity.

What's the difference between $\lim_{x \to a}$ and $\lim_{x \to a^+}$?

$\lim_{x \to a}$ is the two-sided limit (approaching from both directions). $\lim_{x \to a^+}$ is the right-hand limit (only from values greater than $a$). For the two-sided limit to exist, both one-sided limits must exist and be equal.

How do I evaluate limits at infinity?

For rational functions, divide numerator and denominator by the highest power of $x$. Terms like $\frac{1}{x}$ and $\frac{1}{x^2}$ approach 0 as $x \to \infty$. The limit behavior depends on the degrees of the polynomials:

• Same degree → ratio of leading coefficients
• Numerator higher → $\pm\infty$
• Denominator higher → 0

What if L'Hôpital's rule gives another indeterminate form?

Apply it again! Some limits require multiple applications. Example: $\lim_{x \to \infty} \frac{x^2}{e^x}$ gives $\frac{\infty}{\infty}$, so apply L'Hôpital's: $\frac{2x}{e^x}$ (still $\frac{\infty}{\infty}$), apply again: $\frac{2}{e^x} \to 0$ as $x \to \infty$.

Why do we care about limits?

Limits are the foundation of calculus. Derivatives are defined as limits of difference quotients. Integrals are limits of Riemann sums. Continuity is defined using limits. Without limits, there's no calculus—and without calculus, modern science and engineering would be impossible.

How do I know which limit technique to use?

Follow this decision tree:

1. Try direct substitution first. If it works, you're done.
2. If you get $\frac{0}{0}$, try factoring or rationalizing.
3. If that doesn't work, try L'Hôpital's rule.
4. For limits at infinity, divide by highest power of $x$.
5. For oscillating functions, consider squeeze theorem.

Practice builds intuition for recognizing which technique applies.

Can all limits be evaluated algebraically?

Most standard calculus limits can be evaluated with the techniques in this guide. However, some limits require advanced methods (series expansions, specialized theorems) or can only be approximated numerically. MathPad's CAS handles these edge cases using rigorous algorithms.

---

✨ Start solving smarter Try Free →

---

Related Topics

Want to deepen your calculus knowledge? Check out these related guides:

• Derivative Calculator with Steps - Limits define derivatives
• Integration Calculator - Integrals are limits of sums
• Khan Academy: Limits - Free video lessons
• Paul's Online Math Notes: Limits - Comprehensive limit guide
• See all MathPad features - AI Tutor, Step Checker, and more

Conclusion

Limits are the gateway to calculus. Master them, and derivatives, integrals, and continuity all make sense. The key skills are:

✓ Recognizing indeterminate forms (when you need advanced techniques) ✓ Choosing the right technique (factoring, L'Hôpital's, squeeze theorem) ✓ Understanding one-sided vs two-sided limits ✓ Interpreting limits at infinity (horizontal asymptotes)

With practice, limit evaluation becomes systematic. You'll quickly recognize which technique applies and execute it automatically.

If you want to accelerate your learning with instant feedback and CAS-verified step-by-step solutions for every limit, try MathPad's free version and experience AI-powered calculus tutoring.

---

Have questions about limits? Contact our team or start solving problems at mathpad.ai/app.