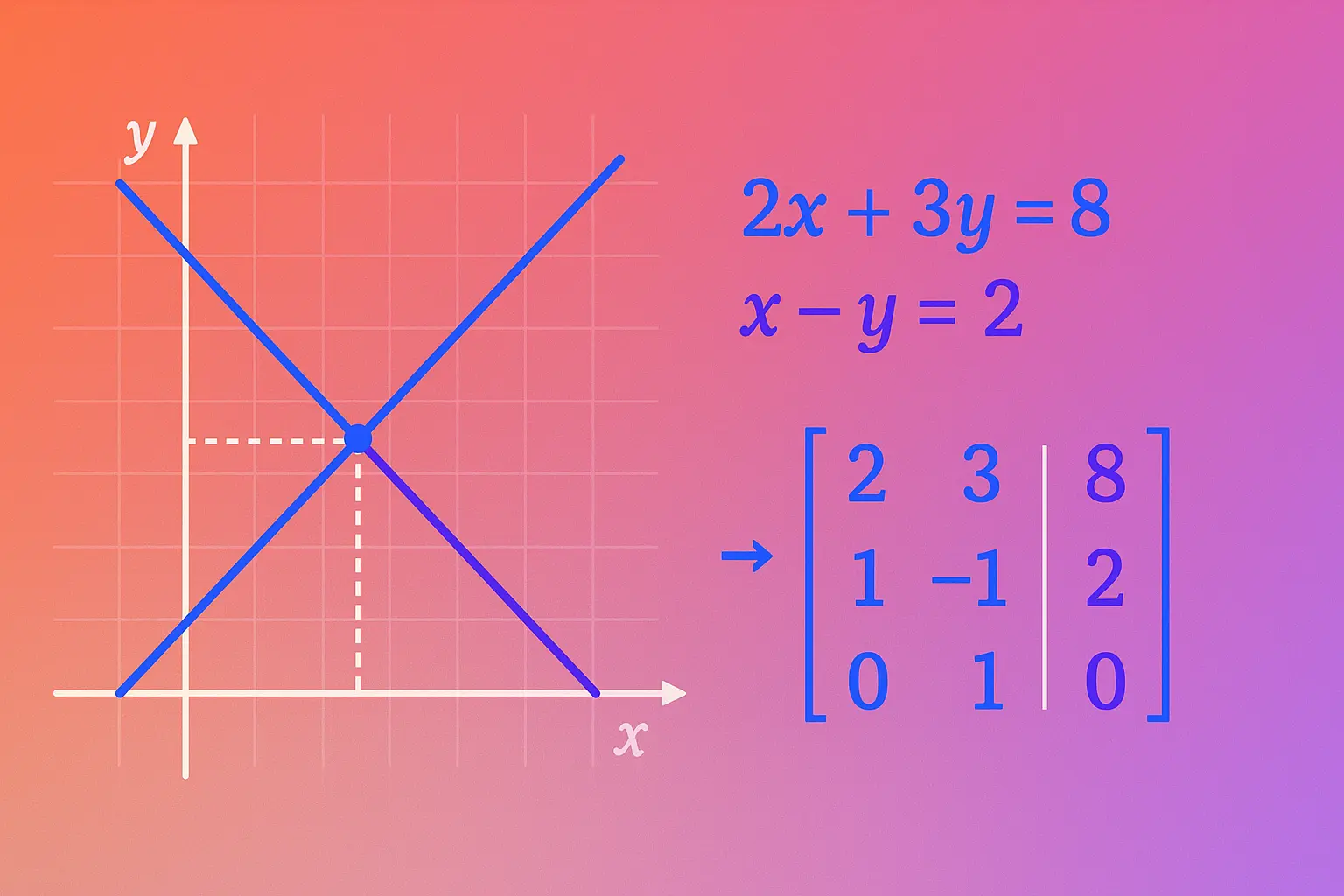Algebra Calculator with Steps: Solve Equations & Simplify Expressions (2025)

📐 Algebra homework piling up? From simple equations like $2x + 5 = 13$ to complex systems and polynomial factoring, algebra is the foundation of all higher mathematics—but it's also where many students get stuck. Whether you're tackling pre-algebra basics or college-level problems, you need more than just answers. You need to understand the process.

In this comprehensive guide, you'll learn what problems an algebra calculator can solve, master key algebraic techniques, avoid common mistakes, and discover how CAS-verified algebra tools catch the errors that pure AI might miss (like sign mistakes and dropped solutions).

🔧 What Can an Algebra Calculator Solve?

A modern algebra calculator is your Swiss Army knife for algebraic manipulation. Here's what it can handle:

Linear Equations

The simplest algebraic equations—isolate the variable to solve:

• One-step: $x + 5 = 12$
• Two-step: $2x + 3 = 11$
• Multi-step with fractions: $\frac{3x - 2}{4} = 5$
• With variables on both sides: $5x + 3 = 2x + 12$

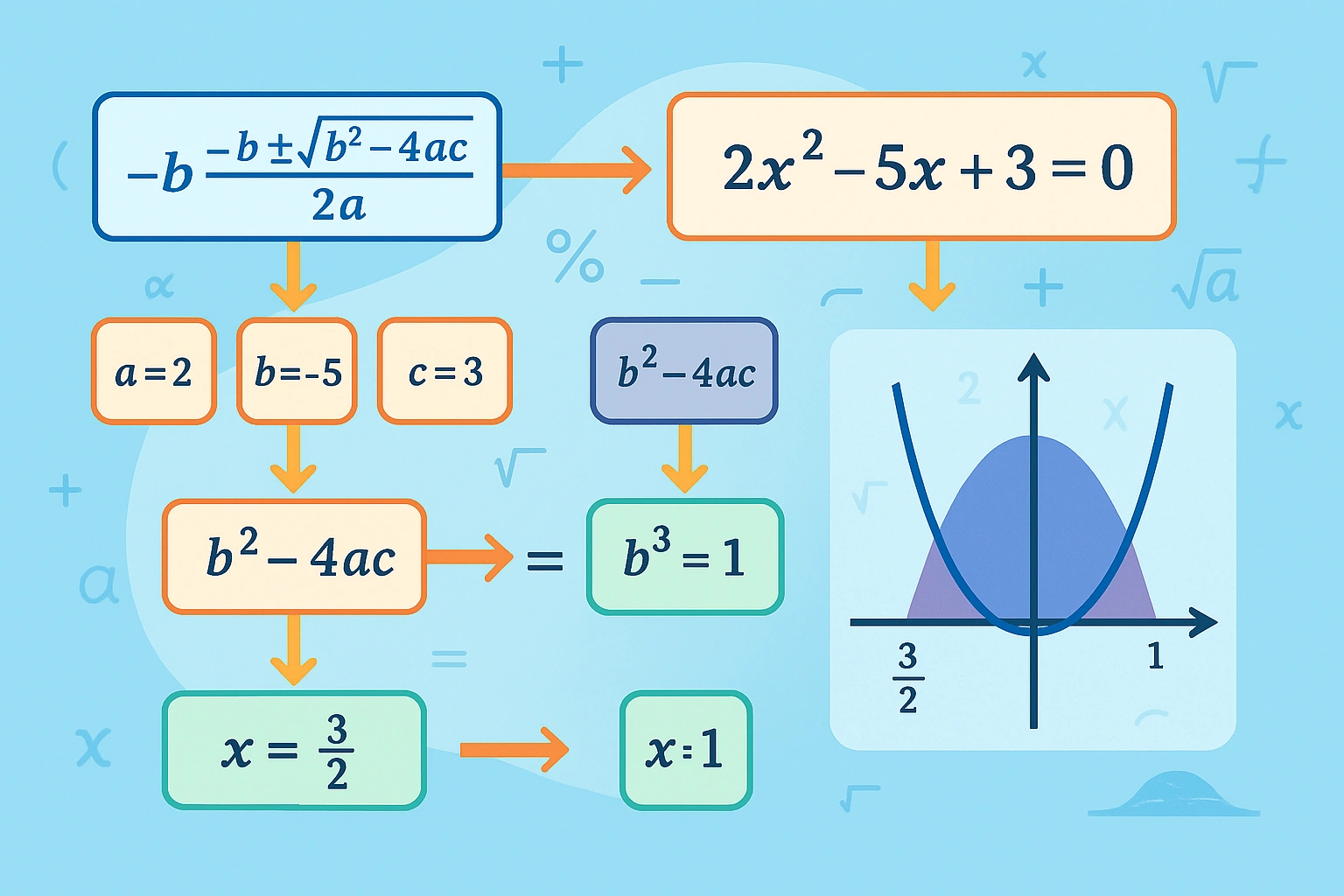
Quadratic Equations

Second-degree polynomial equations—three solution methods:

• Factoring: $x^2 - 5x + 6 = 0 \rightarrow (x-2)(x-3) = 0$
• Quadratic Formula: $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$
• Completing the square: Rewrite as $(x - h)^2 = k$

See our complete guide: Quadratic Formula Calculator →

Systems of Equations

Multiple equations with multiple variables:

• Linear systems ($2 \times 2$, $3 \times 3$, and larger)
• Substitution method: Solve one equation for a variable, substitute
• Elimination method: Add/subtract equations to eliminate variables
• Matrix methods: Use augmented matrices for large systems

Polynomial Operations

Manipulating polynomial expressions:

• Factoring: $x^2 + 5x + 6 = (x+2)(x+3)$
• Expanding: $(x+2)(x+3) = x^2 + 5x + 6$
• Simplifying: $\frac{x^2 - 4}{x - 2} = x + 2$
• Long division: Dividing polynomials

Rational Expressions

Fractions with polynomials:

• Simplifying: $\frac{x^2 - 9}{x + 3} = x - 3$
• Adding/subtracting with common denominators
• Multiplying and dividing rational expressions
• Solving rational equations

Inequalities

Finding solution sets rather than exact values:

• Linear inequalities: $2x + 3 < 11$
• Compound inequalities: $-5 < 2x + 1 < 7$
• Absolute value inequalities: $|x - 3| < 5$
• Quadratic inequalities: $x^2 - 4 < 0$

Absolute Value Equations

Equations involving absolute value (distance from zero):

• Basic: $|x| = 5$ → $x = 5$ or $x = -5$
• Complex: $|2x - 3| = 7$
• With two absolute values: $|x - 1| = |x + 3|$

Radicals and Exponents

Simplifying and solving with roots and powers:

• Simplifying radicals: $\sqrt{50} = 5\sqrt{2}$
• Solving radical equations: $\sqrt{x + 3} = 5$
• Rational exponents: $x^{3/2} = 8$
• Exponential equations: $2^{x+1} = 16$

📚 Types of Algebra Problems (With Detailed Examples)

Let's break down the major categories with complete solutions:

Linear Equations

Example: Multi-Step Equation

Solve: $3(2x - 4) + 5 = 2x + 9$

Solution:

Step 1: Distribute the 3: $$6x - 12 + 5 = 2x + 9$$

Step 2: Combine like terms on the left: $$6x - 7 = 2x + 9$$

Step 3: Subtract $2x$ from both sides: $$4x - 7 = 9$$

Step 4: Add 7 to both sides: $$4x = 16$$

Step 5: Divide by 4: $$x = 4$$

Check: $3(2(4) - 4) + 5 = 3(4) + 5 = 17$ and $2(4) + 9 = 17$ ✓

Key Insight: Always work systematically: distribute, combine, isolate, solve.

Quadratic Equations

Example: Solving by Factoring

Solve: $x^2 - 5x + 6 = 0$

Solution:

Step 1: Factor the quadratic: $$x^2 - 5x + 6 = (x - 2)(x - 3) = 0$$

Step 2: Use the zero product property: $$x - 2 = 0 \text{ or } x - 3 = 0$$

Step 3: Solve each equation: $$x = 2 \text{ or } x = 3$$

Check:

• For $x = 2$: $(2)^2 - 5(2) + 6 = 4 - 10 + 6 = 0$ ✓
• For $x = 3$: $(3)^2 - 5(3) + 6 = 9 - 15 + 6 = 0$ ✓

Alternative Method: Use the quadratic formula: $$x = \frac{5 \pm \sqrt{25 - 24}}{2} = \frac{5 \pm 1}{2}$$

Which gives $x = 3$ or $x = 2$ (same answers!)

Systems of Equations

Example: Substitution Method

Solve the system: $$\begin{cases} 2x + y = 7 \ x - y = 2 \end{cases}$$

Solution:

Step 1: Solve the second equation for $x$: $$x = y + 2$$

Step 2: Substitute into the first equation: $$2(y + 2) + y = 7$$

Step 3: Simplify and solve for $y$: $$2y + 4 + y = 7$$ $$3y + 4 = 7$$ $$3y = 3$$ $$y = 1$$

Step 4: Substitute back to find $x$: $$x = y + 2 = 1 + 2 = 3$$

Solution: $(x, y) = (3, 1)$

Check:

• $2(3) + 1 = 7$ ✓
• $3 - 1 = 2$ ✓

Alternative Method: Elimination (add the equations): $$\begin{align} 2x + y &= 7\ +(x - y &= 2)\ \hline 3x + 0 &= 9\ x &= 3 \end{align}$$

Then substitute back: $y = 1$ (same answer!)

Polynomial Operations

Example: Factoring a Trinomial

Factor: $x^2 + 7x + 12$

Solution:

Step 1: Find two numbers that multiply to 12 and add to 7:

• Factors of 12: (1,12), (2,6), (3,4)
• Which pair adds to 7? $3 + 4 = 7$ ✓

Step 2: Write the factored form: $$x^2 + 7x + 12 = (x + 3)(x + 4)$$

Check: Expand $(x + 3)(x + 4)$: $$= x^2 + 4x + 3x + 12 = x^2 + 7x + 12$$ ✓

Example: Expanding

Expand: $(2x - 3)(x + 5)$

Solution:

Use FOIL (First, Outer, Inner, Last):

• First: $2x \cdot x = 2x^2$
• Outer: $2x \cdot 5 = 10x$
• Inner: $-3 \cdot x = -3x$
• Last: $-3 \cdot 5 = -15$

Combine: $2x^2 + 10x - 3x - 15 = 2x^2 + 7x - 15$

Inequalities

Example: Linear Inequality

Solve: $3x - 5 \leq 10$

Solution:

Step 1: Add 5 to both sides: $$3x \leq 15$$

Step 2: Divide by 3: $$x \leq 5$$

Solution: All real numbers less than or equal to 5

Interval notation: $(-\infty, 5]$

Key Rule: When you multiply or divide by a negative number, flip the inequality sign:

$$-2x < 6 \rightarrow x > -3$$ (sign flipped!)

Absolute Value Equations

Example: Basic Absolute Value

Solve: $|2x - 3| = 7$

Solution:

Absolute value means distance from zero, so we have two cases:

Case 1: $2x - 3 = 7$ $$2x = 10$$ $$x = 5$$

Case 2: $2x - 3 = -7$ $$2x = -4$$ $$x = -2$$

Solutions: $x = 5$ or $x = -2$

Check:

• For $x = 5$: $|2(5) - 3| = |7| = 7$ ✓
• For $x = -2$: $|2(-2) - 3| = |-7| = 7$ ✓

✏️ Step-by-Step Worked Examples

Let's tackle five diverse algebra problems:

Example 1: Multi-Step Linear Equation with Fractions

Problem: Solve $\frac{2x - 3}{5} + \frac{x + 1}{2} = 4$

Solution:

Step 1: Find the common denominator (LCD = 10): $$\frac{2(2x - 3)}{10} + \frac{5(x + 1)}{10} = 4$$

Step 2: Multiply everything by 10 to clear fractions: $$2(2x - 3) + 5(x + 1) = 40$$

Step 3: Distribute: $$4x - 6 + 5x + 5 = 40$$

Step 4: Combine like terms: $$9x - 1 = 40$$

Step 5: Add 1: $$9x = 41$$

Step 6: Divide by 9: $$x = \frac{41}{9}$$

Example 2: System of Equations (Elimination Method)

Problem: Solve: $$\begin{cases} 3x + 2y = 16 \ 5x - 2y = 8 \end{cases}$$

Solution:

Step 1: Notice that the coefficients of $y$ are opposites. Add the equations: $$\begin{align} 3x + 2y &= 16\ +(5x - 2y &= 8)\ \hline 8x + 0 &= 24\ x &= 3 \end{align}$$

Step 2: Substitute $x = 3$ into the first equation: $$3(3) + 2y = 16$$ $$9 + 2y = 16$$ $$2y = 7$$ $$y = \frac{7}{2}$$

Solution: $(x, y) = (3, \frac{7}{2})$

Example 3: Factoring a Trinomial

Problem: Factor $2x^2 + 7x + 3$

Solution:

Step 1: Find two numbers that multiply to $2 \times 3 = 6$ and add to 7:

• Numbers: 6 and 1 (since $6 \times 1 = 6$ and $6 + 1 = 7$)

Step 2: Rewrite the middle term: $$2x^2 + 6x + x + 3$$

Step 3: Factor by grouping: $$2x(x + 3) + 1(x + 3)$$

Step 4: Factor out the common binomial: $$(2x + 1)(x + 3)$$

Check: $(2x + 1)(x + 3) = 2x^2 + 6x + x + 3 = 2x^2 + 7x + 3$ ✓

Example 4: Solving an Inequality

Problem: Solve $-3x + 7 \geq -5$

Solution:

Step 1: Subtract 7 from both sides: $$-3x \geq -12$$

Step 2: Divide by -3 (flip the inequality!): $$x \leq 4$$

Solution: $x \leq 4$ or $(-\infty, 4]$

Visual: All numbers to the left of and including 4 on the number line.

Example 5: Rational Expression Simplification

Problem: Simplify $\frac{x^2 - 9}{x^2 + 6x + 9}$

Solution:

Step 1: Factor the numerator (difference of squares): $$x^2 - 9 = (x - 3)(x + 3)$$

Step 2: Factor the denominator (perfect square trinomial): $$x^2 + 6x + 9 = (x + 3)(x + 3) = (x + 3)^2$$

Step 3: Write the factored form: $$\frac{(x - 3)(x + 3)}{(x + 3)^2}$$

Step 4: Cancel common factors: $$\frac{x - 3}{x + 3} \quad (x \neq -3)$$

Note: We must exclude $x = -3$ because it makes the original denominator zero.

⚠️ Common Algebra Mistakes

These errors trip up even strong students. Watch out for:

Mistake 1: Sign Errors When Distributing

Wrong: $-2(x - 3) = -2x - 6$ Right: $-2(x - 3) = -2x + 6$

Remember: Distribute the negative to BOTH terms inside the parentheses.

Mistake 2: Forgetting to Flip Inequality Signs

Wrong: $-2x < 6 \rightarrow x < -3$ Right: $-2x < 6 \rightarrow x > -3$ (flipped!)

Rule: When multiplying or dividing both sides of an inequality by a negative number, flip the direction of the inequality.

Mistake 3: Incorrect Order of Operations

Wrong: $2 + 3 \times 4 = 5 \times 4 = 20$ Right: $2 + 3 \times 4 = 2 + 12 = 14$

Remember PEMDAS:

• Parentheses
• Exponents
• Multiplication and Division (left to right)
• Addition and Subtraction (left to right)

Mistake 4: Losing Solutions in Rational Equations

Problem: Solve $\frac{1}{x} + \frac{1}{x-2} = \frac{2}{x(x-2)}$

Wrong approach: Multiply by $x(x-2)$ without checking restrictions, potentially getting $x = 0$ or $x = 2$ as "solutions" (which make denominators zero!)

Right approach:

1. Note restrictions: $x \neq 0$ and $x \neq 2$
2. Multiply by LCD: $x(x-2)$
3. Solve the resulting equation
4. Check that solutions don't violate restrictions

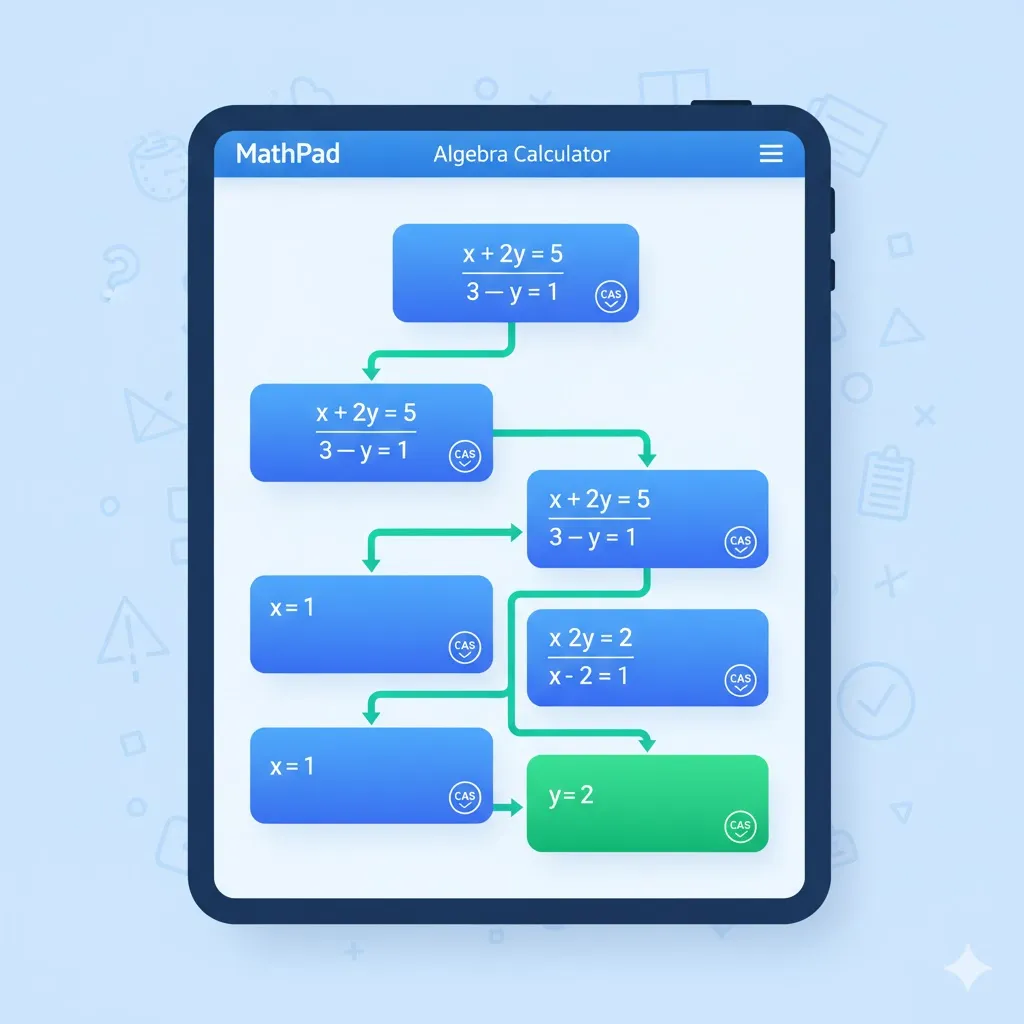
Using MathPad's Algebra Solver

Modern algebra calculators do more than compute—they help you learn. Here's why MathPad stands out:

CAS-Verified Algebraic Manipulation

The Problem with Pure AI: Language models can make algebra errors because they guess patterns rather than compute symbolically. They might:

• Make sign errors when distributing negatives
• Drop solutions (forgetting $x = -2$ when solving $x^2 = 4$)
• Make mistakes in multi-step simplifications
• Incorrectly apply algebraic rules

MathPad's Solution: Every algebraic step is symbolically verified by a Computer Algebra System (CAS):

1. AI proposes a solution method
2. CAS verifies each algebraic transformation symbolically
3. If any step is wrong, CAS catches it
4. You only see mathematically verified, accurate solutions

This means no sign errors, no dropped solutions, no distribution mistakes. Every step is verified before you see it. Learn more about our accuracy approach →

Step Checker: The Homework Verification Tool

This feature is perfect for algebra because algebraic manipulation has many steps where errors creep in:

How it works:

1. Work through your algebra problem by hand (on paper or whiteboard)
2. Photo your work with your phone
3. MathPad's Step Checker analyzes each step
4. See exactly where your logic went wrong (if anywhere)

Perfect for:

• Verifying homework before submission
• Finding the exact step where you made an error
• Understanding why your answer differs from the answer key
• Building confidence in your algebraic skills

Example: You're solving $2(x - 3) = 4$ and get $x = 5$. Step Checker shows:

• ✓ Step 1: Distribute: $2x - 6 = 4$
• ✓ Step 2: Add 6: $2x = 10$
• ✓ Step 3: Divide by 2: $x = 5$

All steps verified!

SnapSolve for Textbook Problems

Don't waste time typing complicated algebra problems:

• Photo textbook problems directly
• Math-specific OCR reads equations, fractions, exponents
• Get step-by-step CAS-verified solutions
• Works with handwritten practice problems too

AI Tutor for Algebra Concepts

Got questions about the process?

• "Why did you factor instead of using the quadratic formula?"
• "How do I know when to use substitution vs elimination?"
• "What's the difference between an equation and an expression?"
• "Can you explain why we flip the inequality sign?"

Get instant, conversational explanations tailored to your level.

Problem Generator for Unlimited Practice

The best way to master algebra: practice. MathPad's Problem Generator creates:

• Unlimited algebra problems at any difficulty level
• Focus on specific topics (just linear equations, just factoring, just systems)
• Each problem comes with complete step-by-step CAS-verified solutions
• Track your progress and identify weak areas

Coverage: Pre-Algebra Through College Algebra

MathPad handles the full algebra spectrum:

• Pre-Algebra: Basic equations, integer operations
• Algebra I: Linear equations, systems, polynomials, factoring
• Algebra II: Quadratics, radicals, rational expressions, exponential equations
• College Algebra: Polynomial division, complex rational expressions, advanced systems

Algebra Calculator vs Doing It By Hand

When to use a calculator:

• ✓ Checking your work before submitting homework
• ✓ Learning step-by-step solution methods
• ✓ Verifying answers on practice problems
• ✓ Understanding why you got a problem wrong
• ✓ Saving time on tedious calculations

When to practice by hand:

• ✓ Preparing for exams (where calculators aren't allowed)
• ✓ Building fluency with algebraic manipulation
• ✓ Developing pattern recognition skills
• ✓ Strengthening mental math abilities

The best approach: Use both strategically. Practice by hand to build skills, then verify with CAS to catch errors and learn from mistakes. This combination builds both speed (from practice) and accuracy (from verification).

Practice Problems

Test your algebra skills:

Linear Equations

1. $4x - 7 = 3x + 5$
2. $\frac{2x + 3}{5} = \frac{x - 1}{3}$

Quadratic Equations

3. $x^2 - 7x + 12 = 0$ (solve by factoring)
4. $2x^2 + 5x - 3 = 0$ (solve using quadratic formula)

Systems of Equations

5. $\begin{cases} x + 2y = 5 \ 3x - y = 4 \end{cases}$ (substitution)
6. $\begin{cases} 2x + 3y = 8 \ 4x + 6y = 16 \end{cases}$ (check for special cases!)

Polynomial Operations

7. Factor: $x^2 - 16$
8. Expand: $(3x - 2)^2$

Inequalities

9. $5x + 3 \geq 18$
10. $-4x < 12$

Ready to check your answers? Use MathPad's algebra calculator to see step-by-step CAS-verified solutions. Try it now →

Frequently Asked Questions

What types of algebra can this solve?

MathPad handles pre-algebra through college algebra:

• Linear equations (one variable, two variables, systems)
• Quadratic equations (all solution methods)
• Polynomial operations (factoring, expanding, simplifying)
• Rational expressions and equations
• Inequalities (linear, quadratic, absolute value)
• Radical equations
• Exponential and logarithmic equations
• Systems of equations (any size)

Is using an algebra calculator cheating?

It depends on how you use it:

✗ Cheating: Copying answers without understanding the process

✓ Learning:

• Checking your work after solving by hand
• Learning solution methods step-by-step
• Understanding where you made a mistake
• Verifying practice problem answers

Think of it like a tutor: Using a tutor to learn isn't cheating, but having them do your homework is. Use algebra calculators the same way—as a learning tool, not a shortcut to avoid thinking.

How do I solve systems of equations?

Three main methods:

1. Substitution (best when one equation is already solved for a variable):

   • Solve one equation for one variable
   • Substitute into the other equation
   • Solve for the remaining variable
   • Back-substitute to find the first variable

2. Elimination (best when coefficients align nicely):

   • Multiply equations to make coefficients of one variable opposites
   • Add equations to eliminate that variable
   • Solve for the remaining variable
   • Back-substitute

3. Matrix methods (best for 3+ variables):

   • Write augmented matrix
   • Use row operations (Gaussian elimination)
   • Back-substitute to find solutions

MathPad shows you all methods and explains which is most efficient for your specific system.

What's the difference between factoring and expanding?

Factoring breaks down an expression into a product of simpler factors: $$x^2 + 5x + 6 \rightarrow (x + 2)(x + 3)$$

Expanding multiplies out factors to get a sum: $$(x + 2)(x + 3) \rightarrow x^2 + 5x + 6$$

They're inverse operations—like multiplication and division. Factoring is generally harder because you must recognize patterns.

How do I check my algebra work?

Method 1: Substitute back (for equations)

• Take your solution and substitute it into the original equation
• If both sides are equal, you're correct
• Example: If $x = 3$ solves $2x + 5 = 11$, check: $2(3) + 5 = 11$ ✓

Method 2: Use Step Checker

• Photo your work
• MathPad verifies each algebraic step
• See exactly where any errors occur

Method 3: Work backward (for simplification)

• If you simplified $\frac{x^2-4}{x-2}$ to $x+2$, expand $x+2$ using $(x-2)$ to verify

Can it solve word problems?

Partially. MathPad excels at:

• Solving the equations after you've set them up
• Showing step-by-step solutions for algebraic parts
• Verifying your equation setup is correct

What it can't do (yet):

• Read a word problem and automatically set up equations
• Interpret ambiguous language without context
• Make judgment calls about real-world constraints

Best practice: Set up your own equations from word problems, then use MathPad to solve them and verify your work.

What's the order of operations for algebra?

PEMDAS (or BODMAS):

1. Parentheses (or Brackets)
2. Exponents (or Orders)
3. Multiplication and Division (left to right, same priority)
4. Addition and Subtraction (left to right, same priority)

Critical mistake: Multiplication doesn't automatically come before division—they have equal priority and are done left to right. Same with addition and subtraction.

Example: $12 \div 3 \times 2 = 4 \times 2 = 8$ (NOT $12 \div 6 = 2$)

How do I know if I should factor or use the formula?

For quadratic equations ($ax^2 + bx + c = 0$):

Try factoring first if:

• $a = 1$ (leading coefficient is 1)
• $c$ is a small integer
• You can quickly spot factors of $c$ that add to $b$

Use the quadratic formula if:

• Factoring isn't obvious after 30 seconds
• $a \neq 1$ and $c$ is large
• The discriminant suggests irrational or complex solutions
• You want to be absolutely sure you're right

Why? Factoring is faster when it works, but the quadratic formula always works. See our quadratic formula guide →

What's the difference between equations and expressions?

Expression: A mathematical phrase that can be simplified but not solved

• Example: $3x + 5$ or $(x + 2)(x - 1)$
• You can simplify, evaluate at a point, or factor it
• No equals sign

Equation: A statement that two expressions are equal

• Example: $3x + 5 = 14$ or $x^2 = 25$
• You can solve it to find values of the variable
• Has an equals sign

Analogy: An expression is like a phrase ("the red car"), while an equation is like a sentence ("the red car is fast").

How does CAS verify algebra steps?

CAS (Computer Algebra System) performs exact symbolic computation:

1. Parses your equation into a symbolic expression tree
2. Applies algebraic rules exactly (not by pattern-guessing)
3. Verifies each transformation is mathematically valid:
   • When distributing: checks every term
   • When factoring: verifies by expanding back
   • When simplifying: confirms expressions are equivalent
4. Catches errors before showing you:
   • Sign errors from distributing negatives
   • Dropped solutions (like forgetting negative roots)
   • Invalid algebraic manipulations

This is why CAS-verified solutions are more reliable than pure AI, which can confidently give you wrong answers. See our accuracy page →

Can it handle inequalities?

Yes! MathPad solves:

• Linear inequalities: $3x - 5 < 10$
• Compound inequalities: $-5 \leq 2x + 1 < 7$
• Absolute value inequalities: $|x - 3| \geq 5$
• Quadratic inequalities: $x^2 - 4 < 0$

For each, you'll see:

• Step-by-step algebraic solution
• Final answer in inequality notation ($x < 5$)
• Interval notation ($(-\infty, 5)$)
• Number line graph (visual representation)

Does it work for pre-algebra and college algebra?

Absolutely. MathPad covers:

Pre-Algebra:

• Basic equations ($x + 5 = 12$)
• Integer operations
• Fractions and decimals in equations
• Simple word problems

Algebra I:

• Linear equations and systems
• Basic polynomials
• Factoring trinomials
• Introduction to quadratics

Algebra II:

• Advanced quadratics
• Radicals and rational exponents
• Rational expressions
• Exponential and logarithmic equations

College Algebra:

• Polynomial long division
• Complex rational expressions
• Systems with 3+ variables
• Advanced factoring techniques

All solutions are CAS-verified regardless of difficulty level.

🔗 Related Topics

Want to explore more math tools?

• Quadratic Formula Calculator - Master quadratic equations specifically
• Derivative Calculator - Calculus uses algebra extensively
• Integration Calculator - Advanced calculus with algebraic techniques
• Features Overview - See all MathPad capabilities
• Khan Academy Algebra - Free video lessons on algebra concepts

❓ FAQ

Is the algebra calculator free to use?

Yes, MathPad offers a free tier with limited daily problems. Premium plans start at $14.99/month for unlimited access to all features including step-by-step solutions, AI tutoring, and practice problem generation.

Does this calculator work on mobile devices?

Yes! MathPad works on all modern browsers including mobile devices. You can snap photos of algebra problems on your phone or tablet and get instant solutions with step-by-step explanations.

Can I see the steps, not just the answer?

Absolutely. MathPad shows detailed step-by-step solutions for every algebra problem, explaining the reasoning behind each step. This helps you understand the process, not just memorize answers.

Is using a calculator for homework cheating?

Math calculators are learning tools, like textbooks. The key is using them to understand concepts and check your work, not just copy answers. Try algebra problems yourself first, then use the calculator to verify and learn from any mistakes.

What types of algebra problems can this solve?

MathPad's algebra calculator handles linear equations, systems of equations, polynomials, factoring, quadratic equations, rational expressions, radicals, absolute value equations, and more—from pre-algebra through college algebra.

Conclusion

Algebra is the gateway to all higher mathematics. Master it, and you unlock calculus, statistics, physics, engineering, and more. The key is understanding the process, not just getting answers.

Remember:

✓ Practice strategically: Work by hand, then verify with CAS ✓ Learn from mistakes: Use Step Checker to find exactly where errors occur ✓ Build pattern recognition: The more problems you solve, the faster you'll recognize solution methods ✓ Use CAS verification: Avoid the sign errors and dropped solutions that even strong students make

Whether you're working through pre-algebra or tackling college-level systems of equations, MathPad's algebra calculator gives you step-by-step solutions backed by symbolic verification—so you can learn with confidence.

Ready to solve your first equation? Start with MathPad's CAS-verified algebra calculator →

---

Last updated: January 2025. All algebraic solutions verified using Computer Algebra System (CAS) tools to ensure mathematical accuracy.